[最も共有された！ √] 内心 外心 問題 109371-三角形の重心 内心 外心 問題

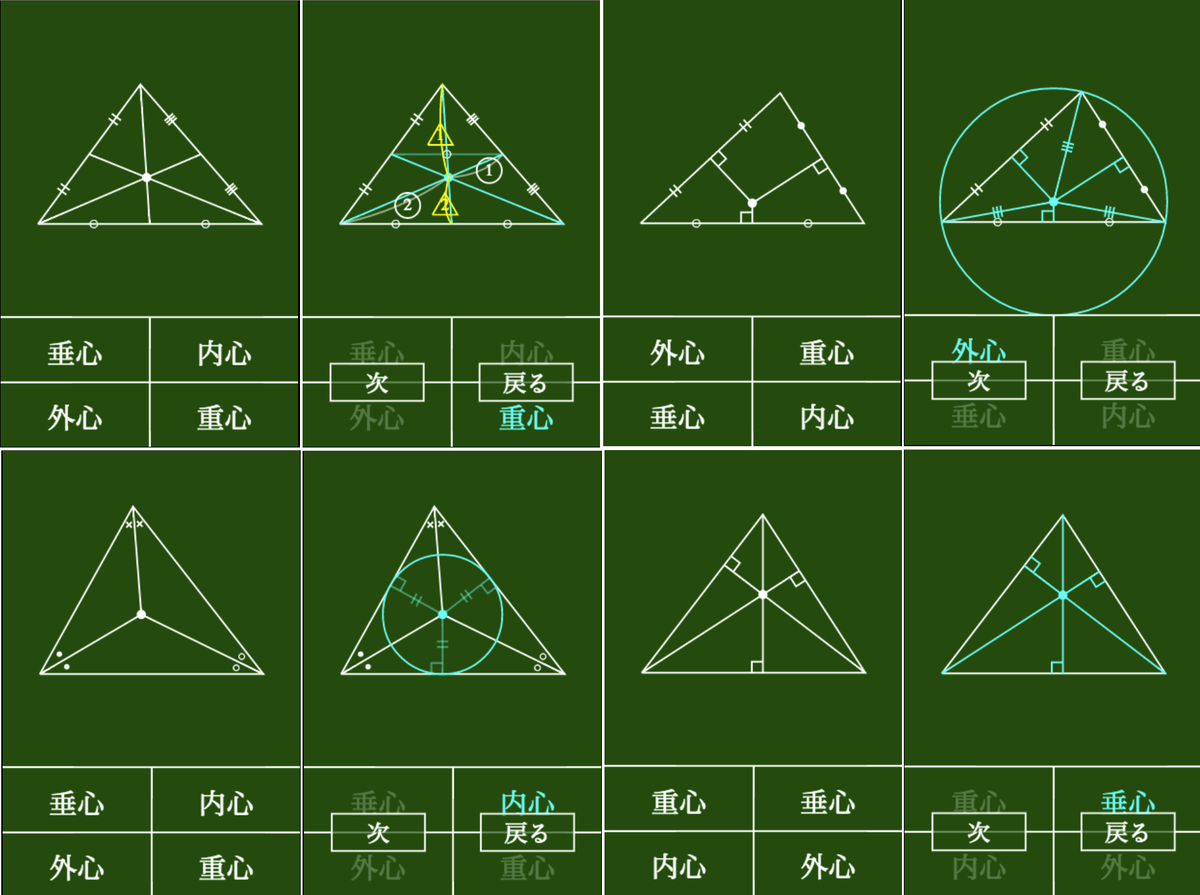
内心 角の二等分線、3 本の交点。 外心 辺の垂直二等分線、3 本の交点。 垂心 3 本の高さ(各頂点からその対辺へ垂直に下ろした線分)の交点。 傍心 三角形の傍接円の中心。Oct 23, 18 · 今回は外心について学習しましょう。外心は図形を扱った問題では頻出です。外心のもつ性質やそれに関わる公式などを使いこなせるようにしておきましょう。 なお、記事の画像が見辛いときはクリックすると拡大できまDec 13, 19 · 外心の特徴、問題の解き方;

数学aの問題で わからない問題が2つほどありまして どう証 人力検索はてな

三角形の重心 内心 外心 問題

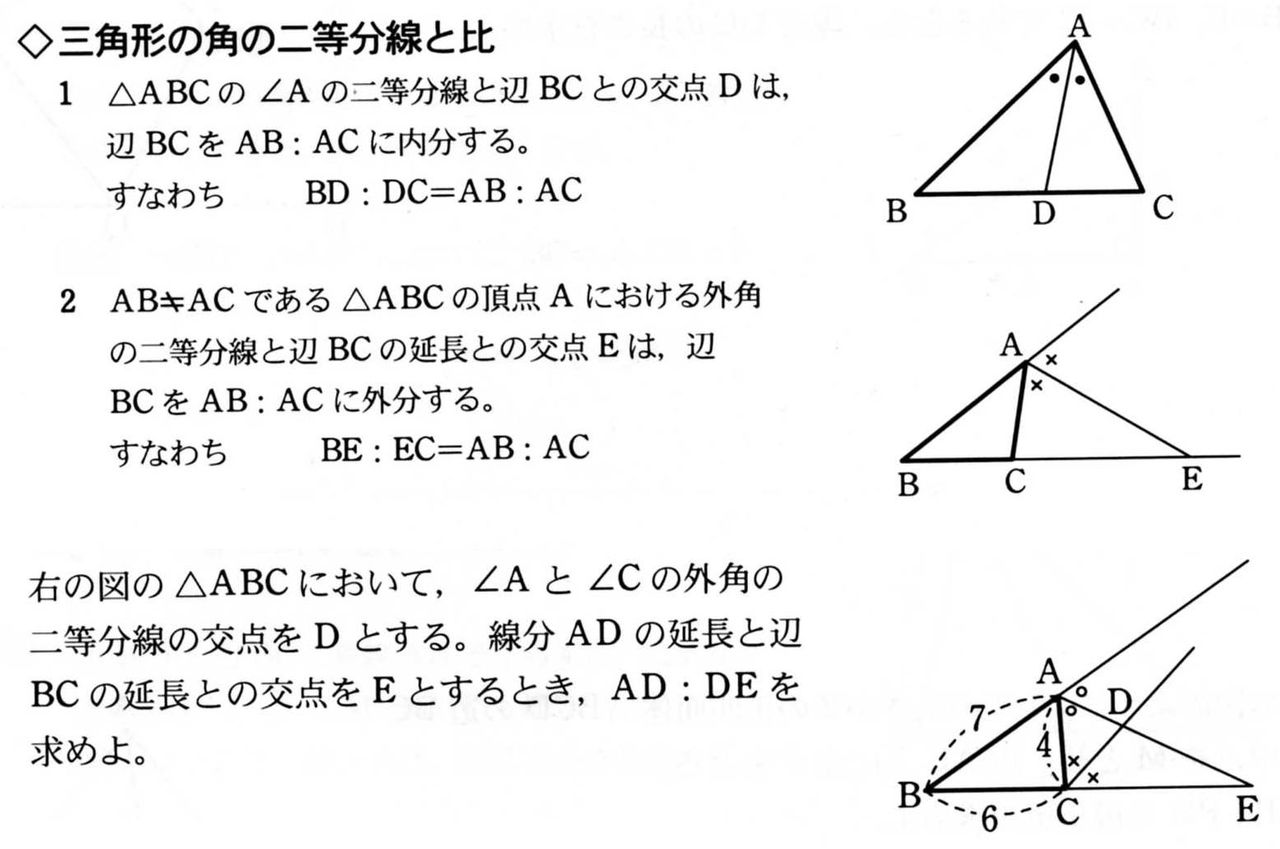
三角形の重心 内心 外心 問題-三角形の内心のベクトルの求め方 三角形ABC の内心をI，辺BC ,C A,AB の長さを, , a b c とする。 求め方1：内角の2 等分線の性質を利用 直線A I と辺B C の交点をD とすると，A I は∠BA C の二等分線だから， BD ：DC ＝AB ：AC ＝c：b よって， AD AB AC b c c b c b = ，B D① 内心と外心の距離 図において，o を abc の外心，i を内心，外 接円の半径を r ，内接円の半径を r ，内心と外心 の距離oi を， oi d とおく （ⅰ）方べきの定理 方べきの定理から (r d)(r d) iauie なので，ia×ie を求めれば d がわかる． （ⅱ） ie＝be を示す

改訂版 3trial数学a P118 ２ 三角形の外心 内心 重心

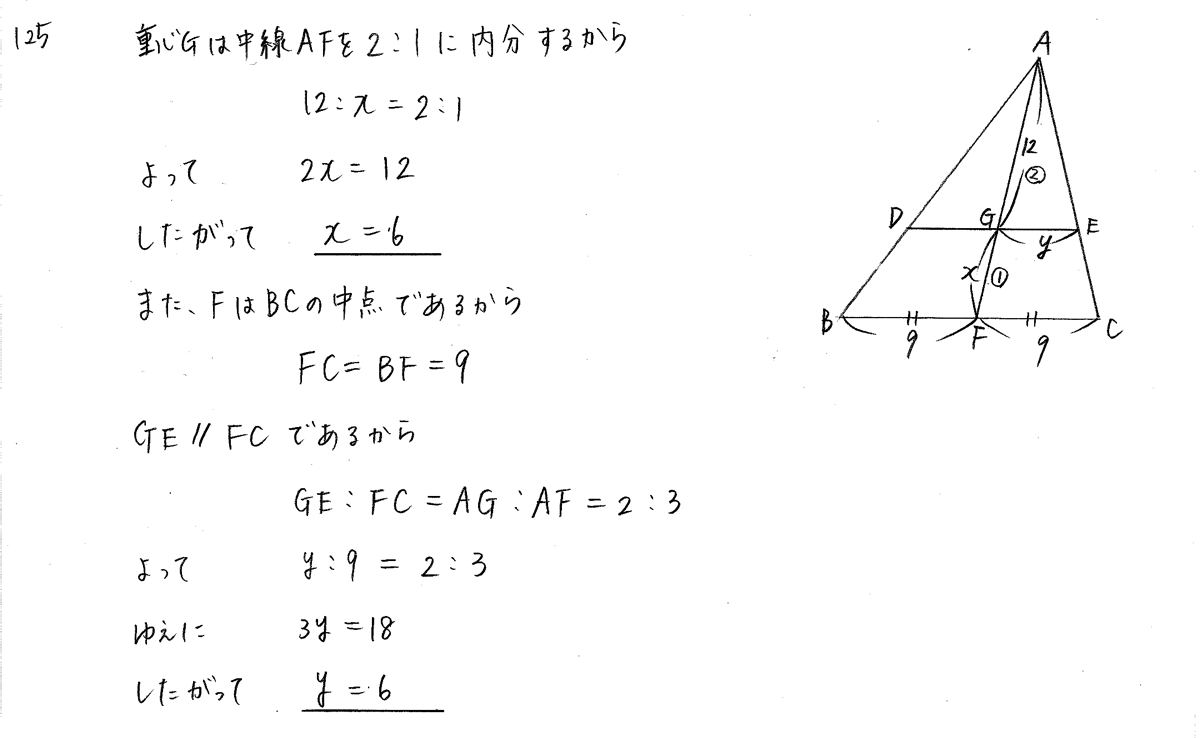
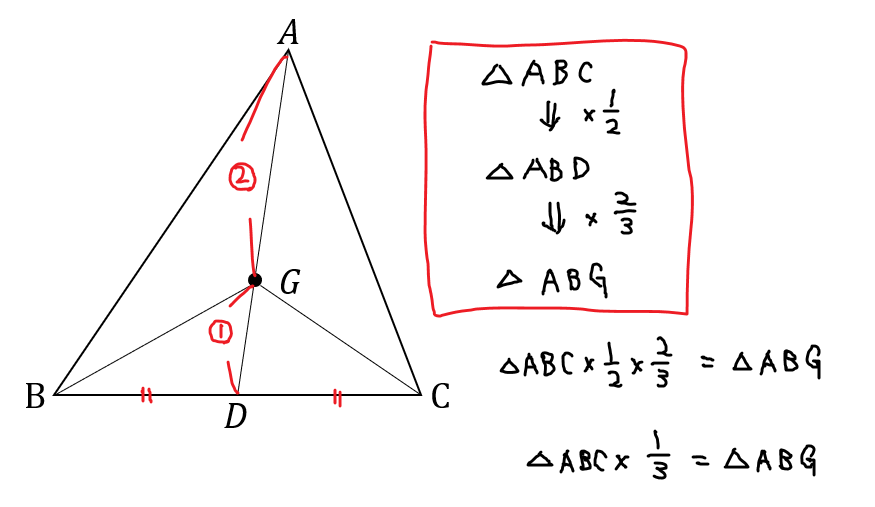
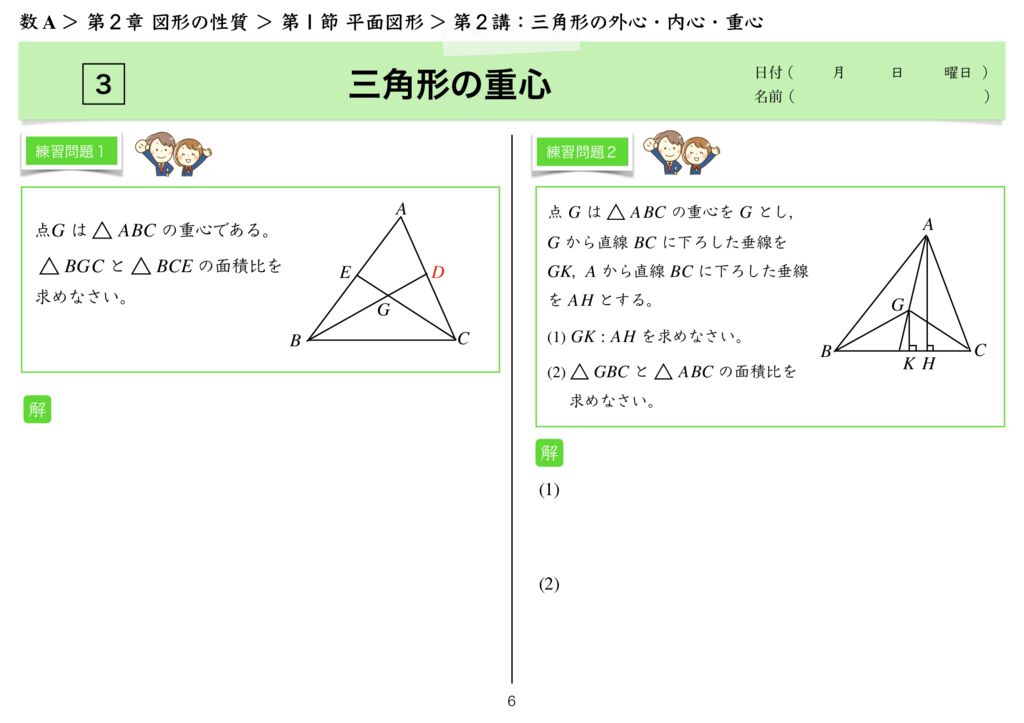
三角形の垂心の証明 三角形の垂心 三角形の各頂点から、対辺またはその延長上に下ろした3本の垂線は、1点で交わる このテキストでは、この定理を証明します。 証明 ABCの各頂点から、対辺に向かって垂線をおろす。（頂点Aからは辺BCに向かって、外心・内心の確認。 外心・内心の意味を確認させ る。 展開 40分 外心・内心の性質を 個人で考察する。 外心・内心の性質を 確認する。 問題を解く。 評価する。 結果発表 まとめ 外心チーム 個人で外心の性質を見つける。 内心チーム数学a 授業プリント# 27 年 組 号 氏名 三角形の重心 b c a n m l g ☆ ☆ 2 2 1 1 2 1 㾻三角形の3 つの中線は、1 点で交わる。 この点 を重心という 㾼重心は、各中線を2 1 に内分する 例題1 右の三角形で点g は4abc の重心である。 このときbl、cg の長さを求めなさい。 b c a n m l g 3 cm

三角形の外心 図の ABCをみてください。 ABCの3つの頂点を通る円を一緒に描いてありますが、この円のことを外接円と呼びます。三角形の周りを囲っている円ですね。 この外接円の中心の点を ABCの外心と呼びます。 この外心は、 ABCの各辺のMar 06, 21 · （→内心と傍心の性質の比較） 外心，重心，垂心は座標やベクトルを用いたゴリ押し計算で扱うこともできますが， 内心，傍心は角度に関する情報が本質的な役割を果たすので解析的なアプローチはほとんどの場合で通用しません。Q 外心をo 内心をiとする。oiを求めよ ab=8 bc=7 ca=5の三角形があり、外心をo 内心をiとする。oiを求めよ。 という問題の解説をどなたかお願いします。 オイラーの定理を使えば簡単なのですが 数iAの問題として出ていたので

今回は図形分野から「重心・外心・内心」です。 これに加えて、垂心と傍心を加えて五心と呼ばれます。 垂心と傍心は出題範囲外になるので、主に上記の 3 つを抑えておく必要があります。内心ー重心の性質は理解できています。 重心の性質、またその性質をどのように問題に活かせばいいのかがわかりません。 解説を読んでもよくわかりません。 よろしくお願い致します。 ｴｵｶがわかりTLT \ t g w elearning Ȋw G Newton m ł H Newton ̊֘A Ђ č œ 擾 TLT \ t g B Z ^ ΍ ܂ ̃ C i b v

Studydoctor三角形の外心 高校数学ａ Studydoctor

角の二等分線と三角形の内心 高校数学に関する質問 勉強質問サイト

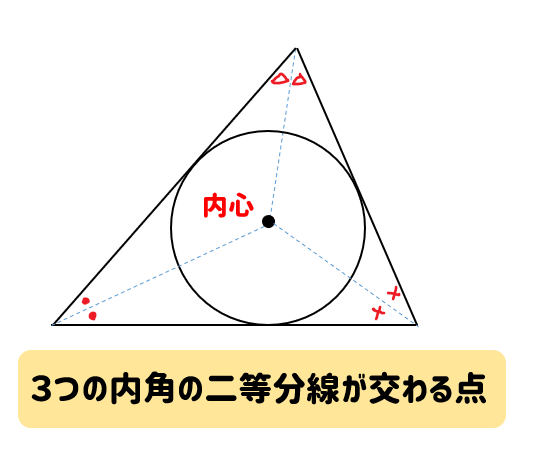
外心 三角形の3辺の垂直二等分線は1点で交わる。この点を外心という。 外心は3つの頂点から等距離にある。(外接円の中心) 内心 三角形の3つの内角の二等分線は1点で交わる。この点を内心という。 内心は3つの辺から等距離にある。(内接円の中心) 重心イズミの解答への道 四面体にも内心、外心が存在します。今回は外心の存在を示します。解答 各頂点を通る球の中心を P 問題複素数 an ( n = 1 , 2 , ) を次のように定める。同問題では，頂点が対辺の一定の側にあるときの内心と傍心の軌跡を問いている。 （2）垂心の軌跡 bcの中点をmとする。外心をoとして，であるから， よって，垂心hの軌跡は abcの外接円と半径が等しく，中心が2omだけ平行移動した円を描く。 （3）重心の軌跡

三角形の外心 内心 重心 垂心 Geogebra

三角形の内心 外心 重心に関するやさしい問題 前期日程大分大学経済学部の入試問題 身勝手な主張

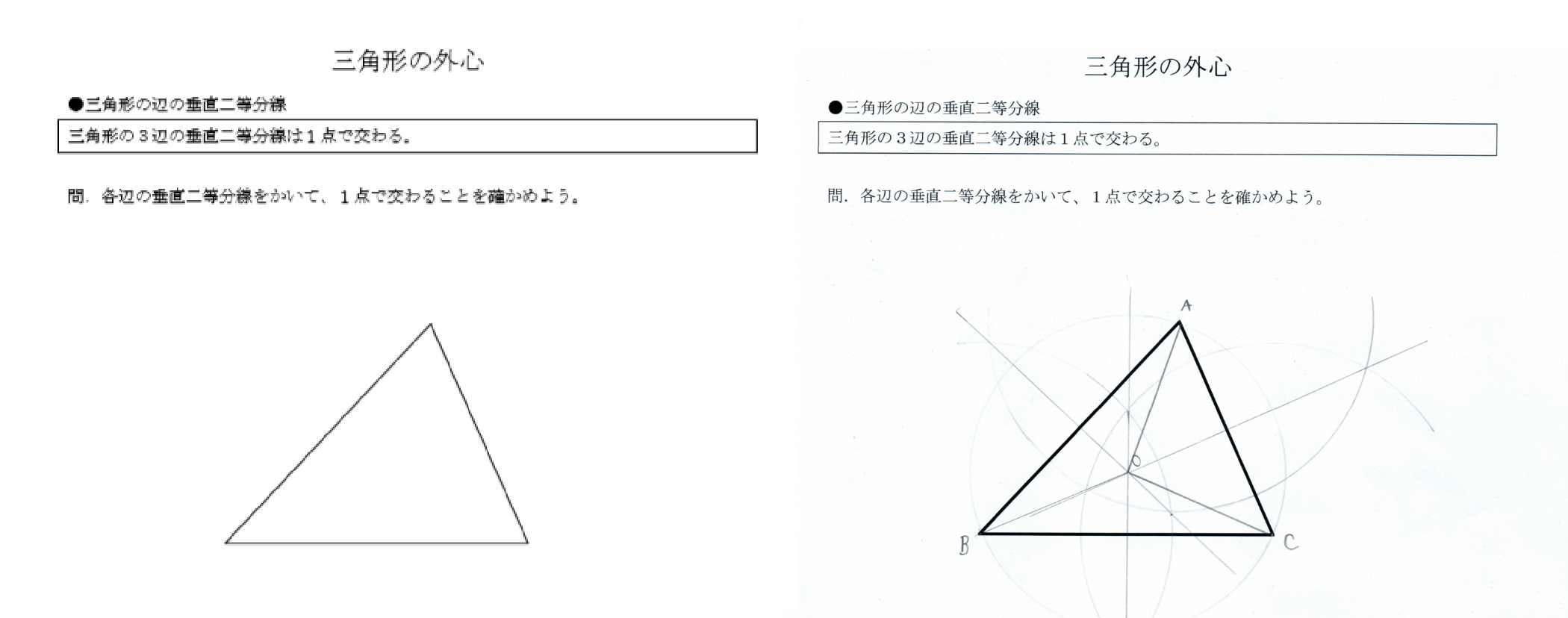
こんにちは、ウチダショウマです。 今日は数学a「図形の性質」で習う 「三角形の外心(垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは困難です。三角形の5心（外心・内心・重心・傍心・垂心）のうち外心について考えていきます。 三角形の各辺の垂直二等分線は 1 点で交わります 。 これは以下のように証明ができます。 において，辺 ， の垂直二等分線の交点を とします。 は の 垂直二等分線上の点なので， ①「ラングレーの問題」の「内心について」のページに「問題3」を追加しました。この問題は京大の入試問題ですが、中学生にもできる大学入試問題かもしれない？ 08 1/2 「ラングレーの問題」の「外心について」のページに「問題」を追加 07

三角形の五心

ねこ騙し数学

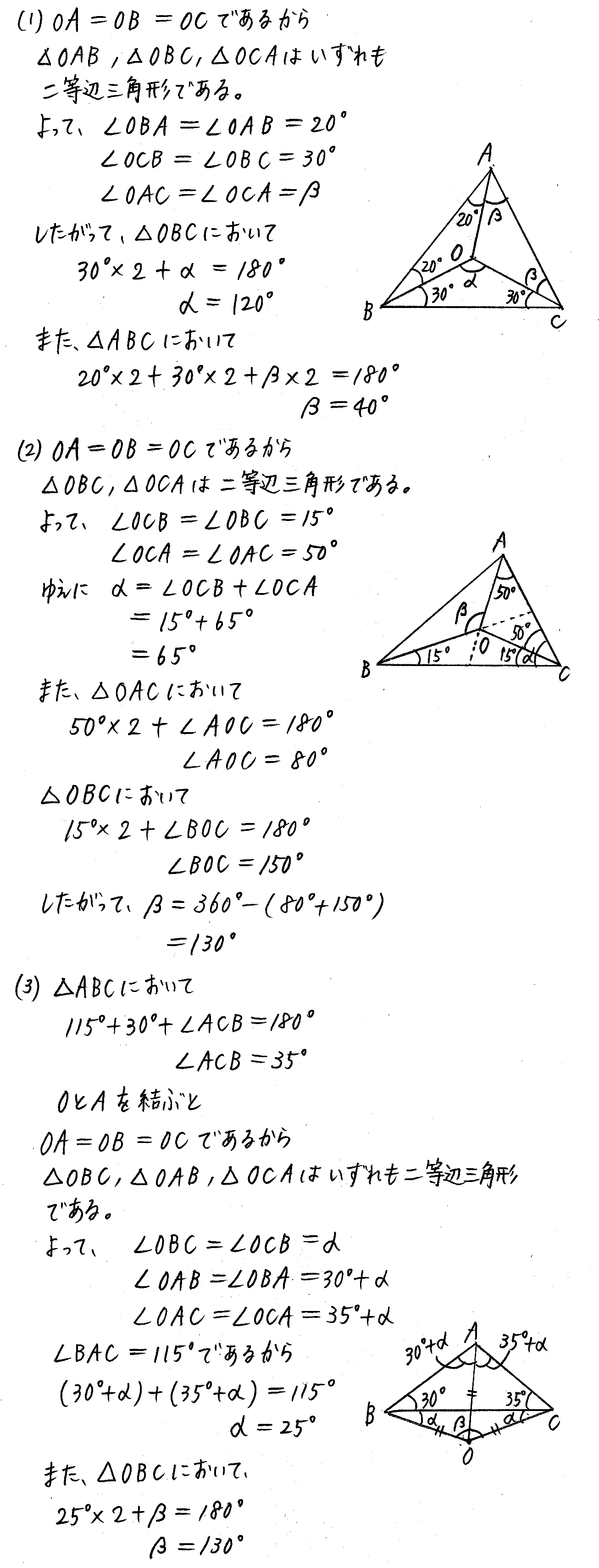
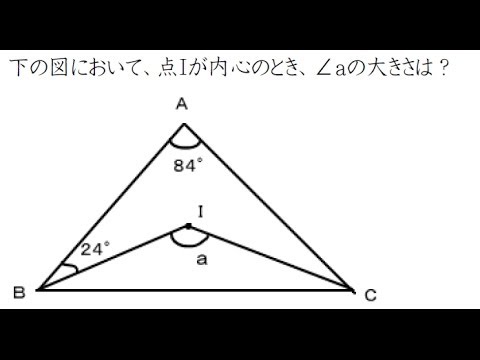
円の五心の基礎ついてまとめました‼ 学年 中学3年生, 単元 円周角の定理(円周角と中心角),円周角の定理の利用, キーワード 垂心,円,外心,内心,円周角前回 https//googl/CwW15I 次回 https//googl/gzjOR0動画のプリント（19ch） http//www19chtv/サブチャンネル とある男が内心・外心 この問題は αの角度を求める問題なんですが、答えが115゜になる意味が解りません(*_*) 私は100゜だと思っていました； ちなみにIは abcの内心だそうです。 回答お願いします。

改訂版 3trial数学a P118 ２ 三角形の外心 内心 重心

高校数学a 三角形の内心2 実践 例題編 映像授業のtry It トライイット

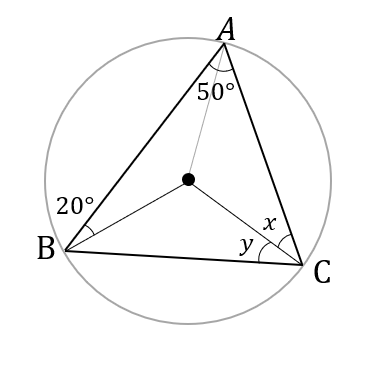
として問題を解いていくのはめんどうなので、 方べきの定理として、辺の関係を覚えておくといいでしょう。 方べきの定理を使って問題を解いてみよう！ それでは、方べきの定理を使った問題に挑戦し内心と傍心の軌跡がどのような曲線となるかについて考察 する。この問題は多くの先人が考察してきたが、軌跡の曲 線群全体については考察されていなかった問題である。 ①研究の背景 三角形の2つの頂点を固定し、もう1つの頂点をある三角形の外心、三角形の外接円 この1点で交わった点 o を三角形の外心という。 外心 o を中心として、半径 oa の円が三角形 abc の外接円である。 oa＝ob＝oc ol⊥bc 、 om⊥ac 、 on⊥ab

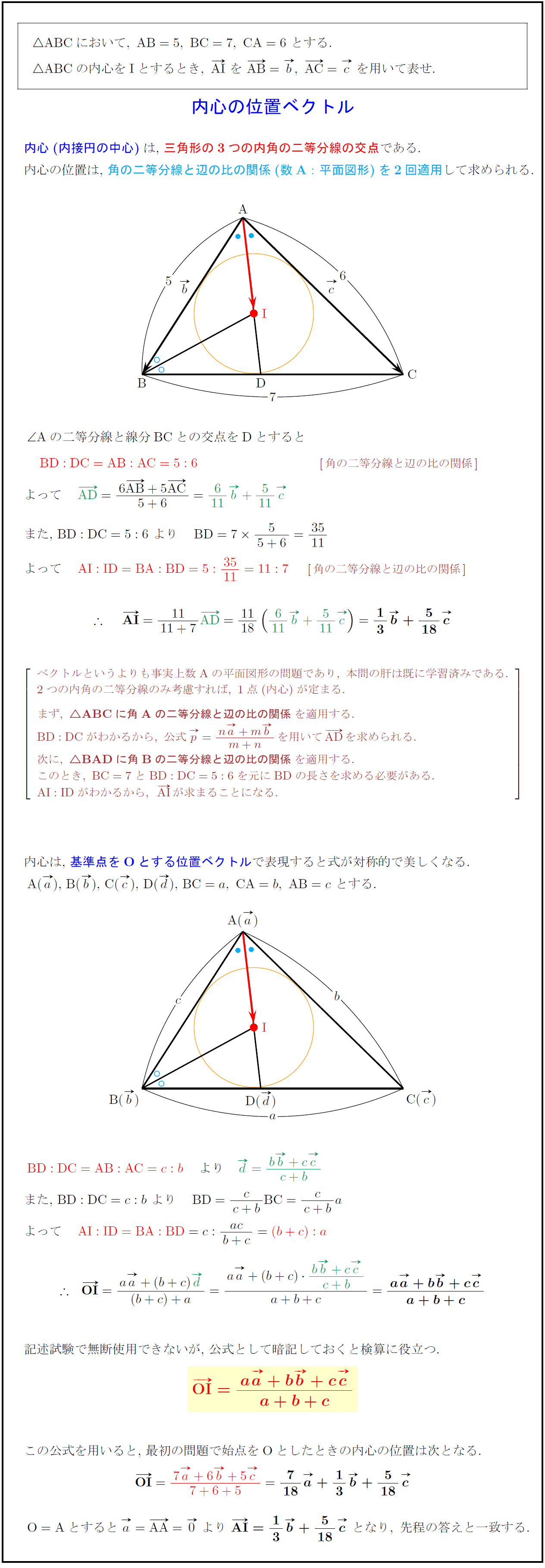
高校数学b 三角形の内心の位置ベクトル 受験の月

三角形の五心

問題 19年度実施「筑駒高入試プレ（中3）」より 問題をpdfで見る 出題者からのひと言 三角形の五心（重心、内心、外心、傍心、垂心）のなかでも普段触れることの少ない三角形の垂心をテーマにした問題外心、内心の基本問題(角度) abcの外心をoとする。角α、βを求めよ。 α β 51° 19° o 答α=70°, β=° o β α 26° 40° 答α=100°, β=24° o α β 41° 18° 答α=59°, β=118° o α β 68° 24° 答α=44°, β=136° o 36° α 答α=54° α 30° 21° 答α=102° abcの内心をiとする。角α、βを求めよ。形の外心，内心，重心の性質や作図の方法を扱い，それらを現実の社会に根ざした問題の考察に活用でき るようにする。 具体的には，「PISA 03年調査の評価の枠組み」に示されている「街灯問題 1 」

五心 重心 内心 外心 垂心 傍心 とは 求め方や性質 受験辞典

平面図形２ 外心 内心 怜悧玲瓏 高校数学を天空から俯瞰する

※ 問題の一例 4 外心と内心の意味を理解する ・教師の説明中心 ・ボロノイの図の考えから外心と内心を説明する ・時間がなければ割愛 ・バスケットボールのディフェンスと内心の関係も説明 本時の学習三角形の外心、内心の問題の質問です。解答はあるのですが、計算過程がないので困っています。以下の問題の解答解説よろしくお願いします。 （1）図1の abcにおいて、辺bcの中点をM、 abcの重心、外心をそれぞれg重要な相互関係 1 正三角形のときは，重心・外心・内心・垂心は一致します． 2 三角形の外接円の半径Rは，内接円の半径rよりも大きくなります．（2倍以上になります．）

高校数学1年の重心 外心 内心 垂心の問題です それぞれの定理はわか Yahoo 知恵袋

高校数学 数a ３６ 三角形の内心 外心 重心 垂心 Youtube

外心，重心，垂心は1直線上にあることを示すことができる．（内心は，これら3点と同一直線上にあるとは限らない） (51)を直接示そうとすると， の 差 を比較することになるが，これらはすでに複雑な三角関数の分数式になっているので，通分などが容易ここからは、 三角形の外心、内心、重心 について学習していこう。外心、内心、重心 は、簡単に言うと、 三角形の中心 のこと。 「三角形の中心」って、見方によって 色々な種類 があり、それぞれ別の点になるんだ。 まずは、 三角形の外心 がどんな点を表すかを解説していくよ。三角形の五心とは、 「内心」「外心」「重心」「垂心」「傍心」の5つの点 です。 この5つの点は、それぞれ定義や性質が異なり、点の書き方も異なります。 「内心」や「重心」は耳にしたことある方も多いと思いますが、「傍心」なんかはマイナーですよね。

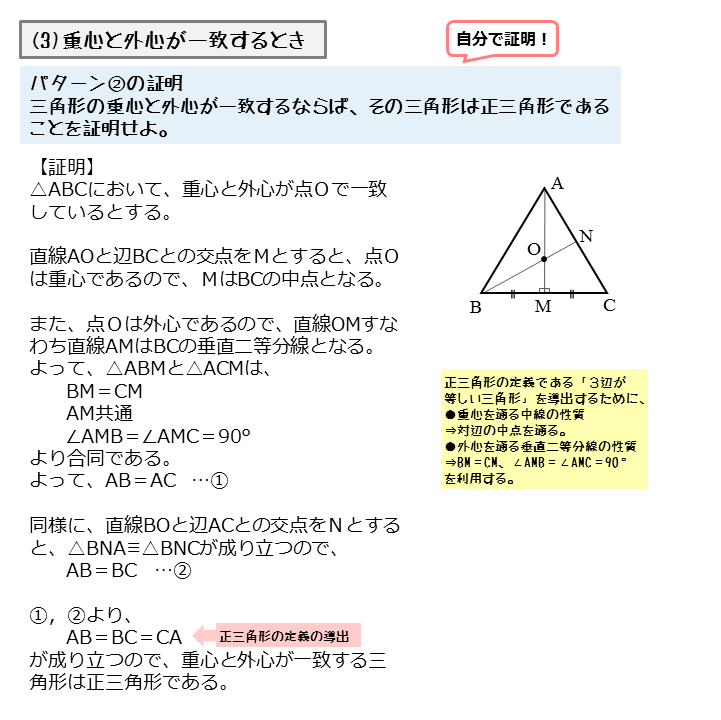
Abcの内心と外心が一致するとき Abcは正三角形であることを証 Yahoo 知恵袋

内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学塾

三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典

三角形の外接円と外心 内接円と内心 中学 高校数学 身勝手な主張

1 Abc P Zbpc C130 P Lihat Cara Penyelesaian Di Qanda

外心 内心 重心 垂心のうち 2つが一致すれば正三角形である 三角形の五心 Youtube

この大きい2と3の問題で Abcの外心と内心の違いを教えて下さい Yahoo 知恵袋

高校数学a 重心 内心 外心 垂心のうち2つが一致する三角形は正三角形であることの証明 受験の月

1 A30 0 Abc I H O Lihat Cara Penyelesaian Di Qanda

五心 重心 内心 外心 垂心 傍心 とは 求め方や性質 受験辞典

数学です 重心 内心 外心です わかる方教えてください 数学です 数学 教えて Goo

数学の三角形の外心内心で 写真の2つの問題を教えてください よろ Yahoo 知恵袋

クリアー数学ａ 数a P118 11 三角形の外心 内心 重心

Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ

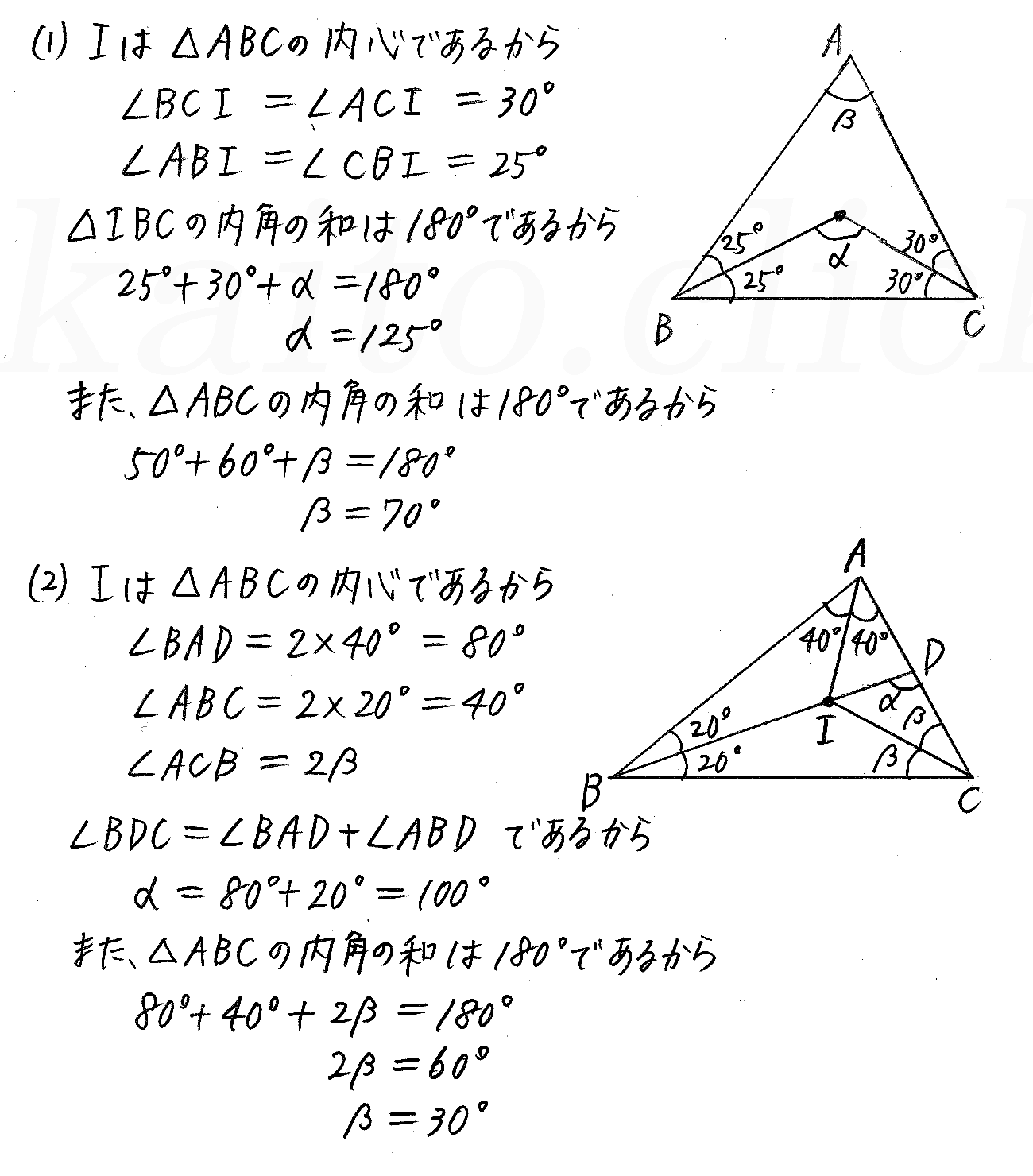
改訂版 4step数学ａ P125 ２ 三角形の外心 内心 重心

内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学塾

外接円 外心について

三角形の外心 高校数学ａ Youtube

外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ

三角形の五心 重心 垂心 外心 内心 傍心 偏差値40から有名大学合格 入試問題を戦略で学ぶ さくら教育研究所 Skredu

この図において 点ｏは Abcの外心である A Bを求めよ この問題が その他 学校 勉強 教えて Goo

三角形の内心 三角形の外心 三角形の重心

図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ

三角形の外心について知っておきたい知識まとめ 理系ラボ

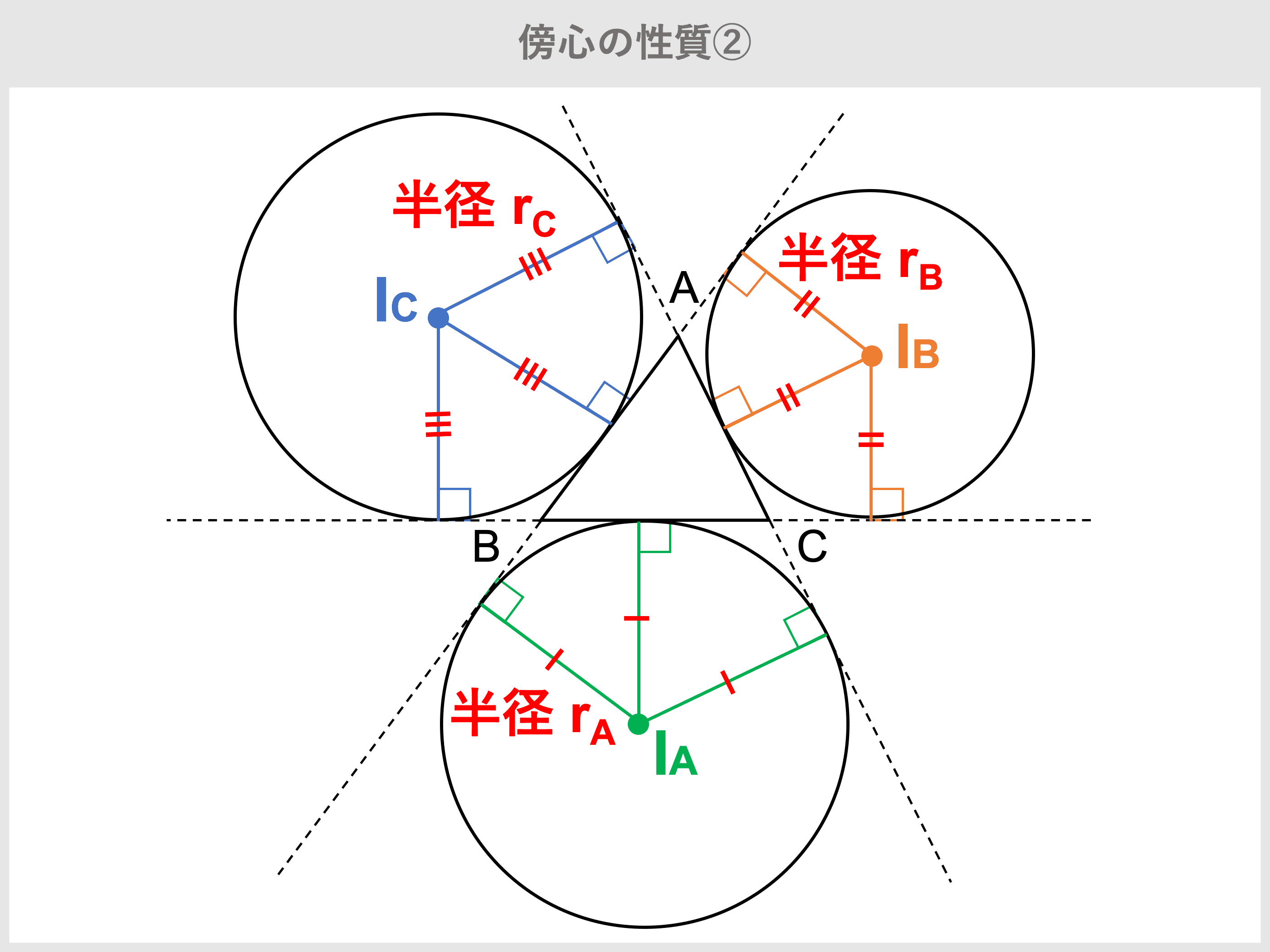
傍心 ぼうしん とは 東大合格コム

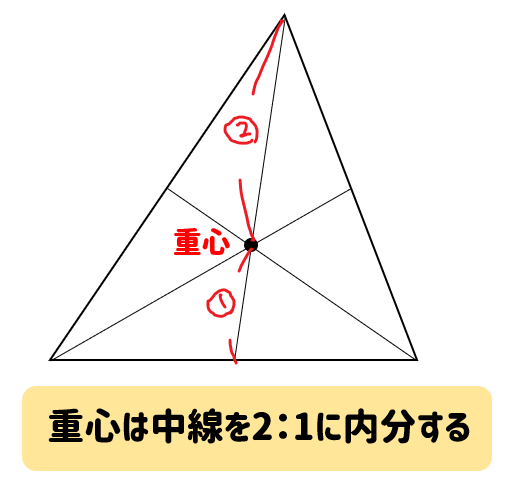
外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ

Studydoctor三角形の内心 高校数学ａ Studydoctor

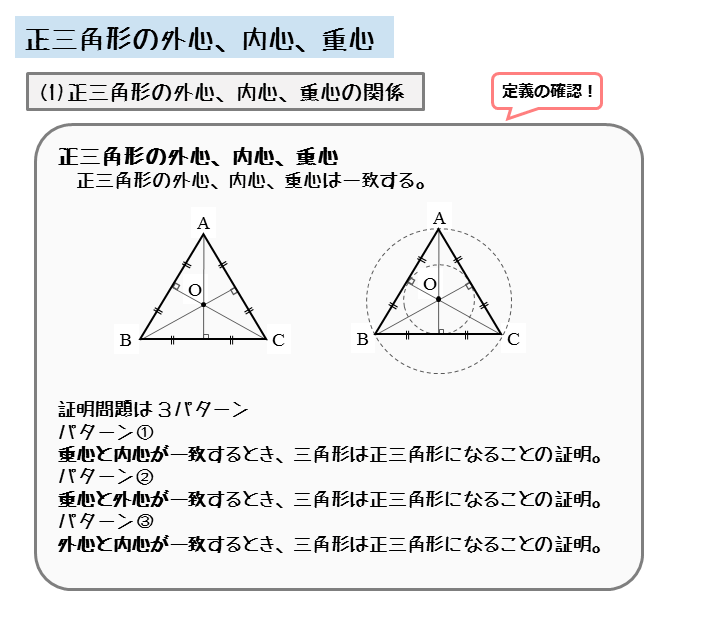
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

高校数学a 三角形の外心2 実践 例題編 映像授業のtry It トライイット

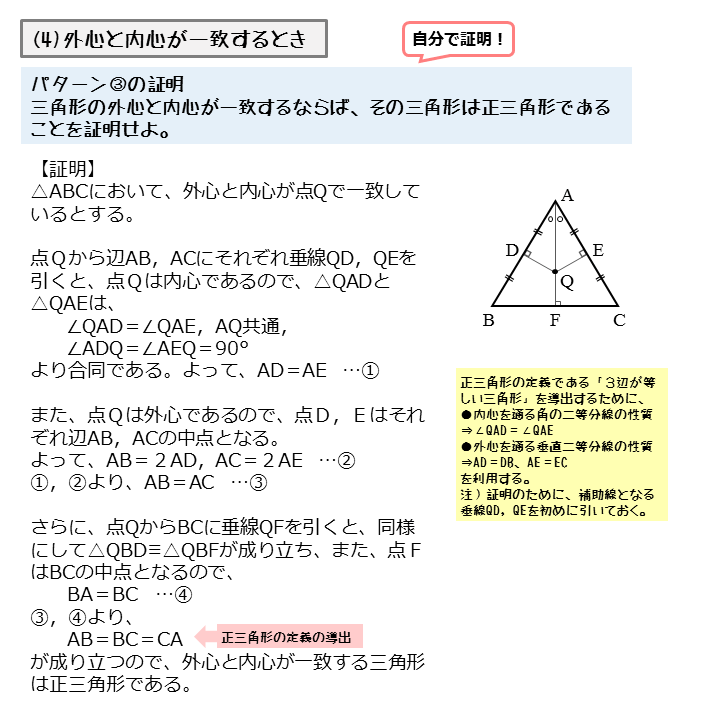
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

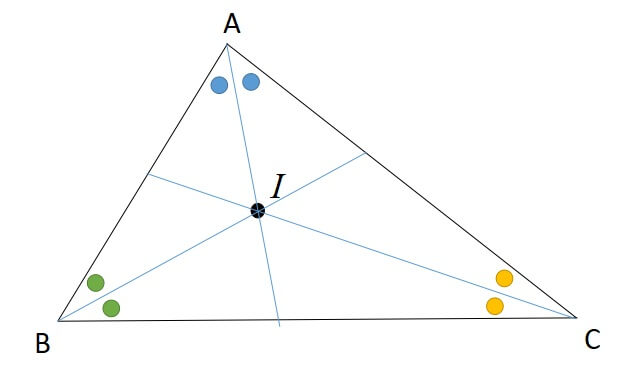
三角形の五心 内心 外心 重心 垂心 傍心 の性質と証明を解説

高校数学a 三角形の外心2 実践 練習編 映像授業のtry It トライイット

数学aの問題で わからない問題が2つほどありまして どう証 人力検索はてな

外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ

外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ

内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学塾

高校数学b ベクトルとオイラー線 三角形の重心g 外心o 垂心hの位置関係 受験の月

Tossランド 作図を取り入れた 三角形の外心 内心 の進め方

Abac15q Abc G I O Lihat Cara Penyelesaian Di Qanda

改訂版 4step数学ａ P125 ２ 三角形の外心 内心 重心

Abcの内心をi A内の傍心をi1とするとき Abcの 高校数学に関する質問 勉強質問サイト

ベクトルの半分が解ける 外心 内心 重心 垂心の位置ベクトル 塾を探す前に読むブログ

Tossランド 三角形の外心 内心 の基礎 基本 ｄｌ可

数学 三角形の内心 高校数学に関する質問 勉強質問サイト

関数星人２ ツー さんのツイート 三角形の内心 外心 重心 垂心 ウェブサイトやアプリでデジタルの力を体感して下さい T Co Ytnzzst9rk T Co Ehpxplgvqw

この問題 3 三本の線が外心を通ればどんな 高校数学に関する質問 勉強質問サイト

三角形の外接円と外心 内接円と内心 中学 高校数学 身勝手な主張

Tossランド 作図を取り入れた 三角形の外心 内心 の進め方

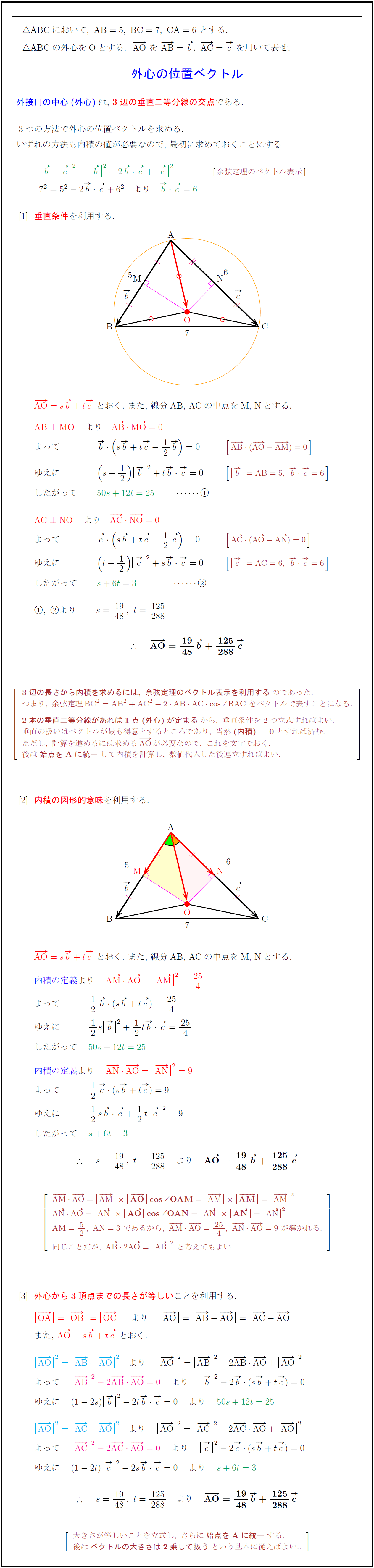
高校数学b 三角形の外心の位置ベクトル 受験の月

外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学塾

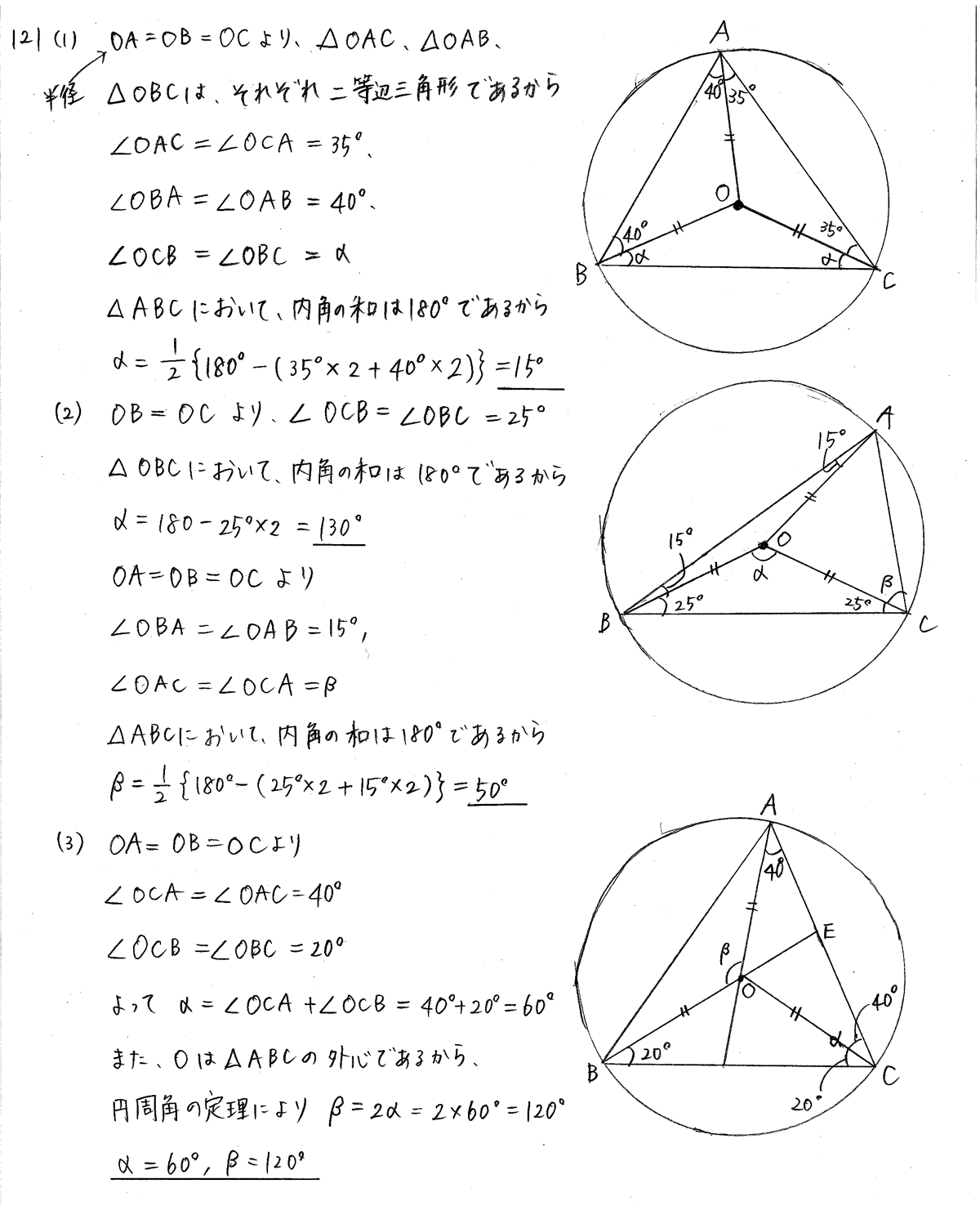
クリアー数学ａ 数a P117 11 三角形の外心 内心 重心

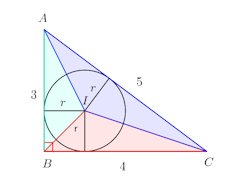
ねこ騙し数学

平面図形２ 外心 内心 怜悧玲瓏 高校数学を天空から俯瞰する

三角形の重心 外心 内心の問題です 計算と答えを教えてくださ Yahoo 知恵袋

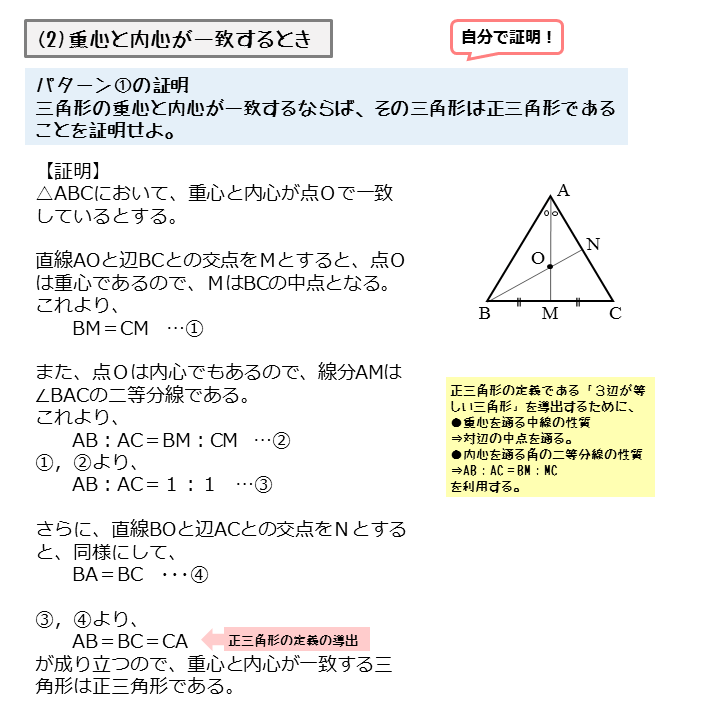
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

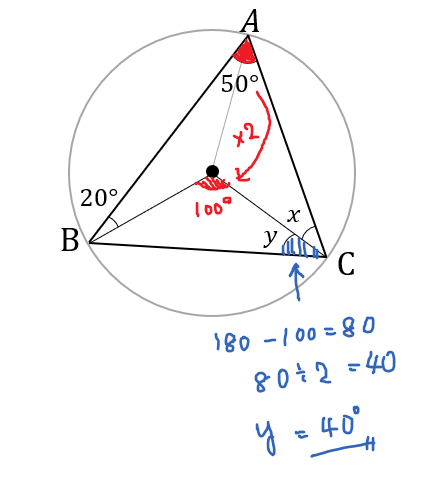
外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ

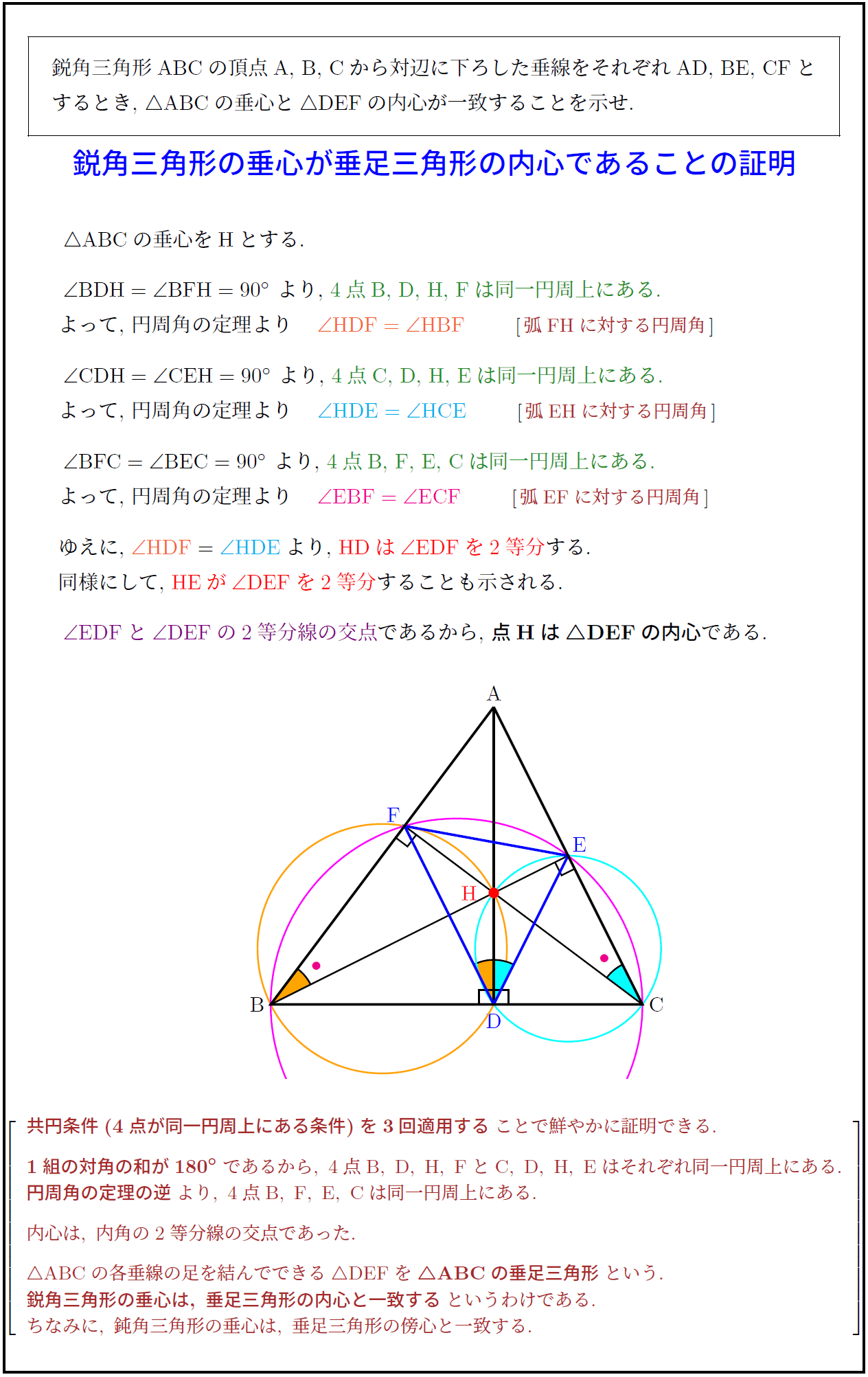
高校数学a 鋭角三角形の垂心が垂足三角形の内心であることの証明 受験の月

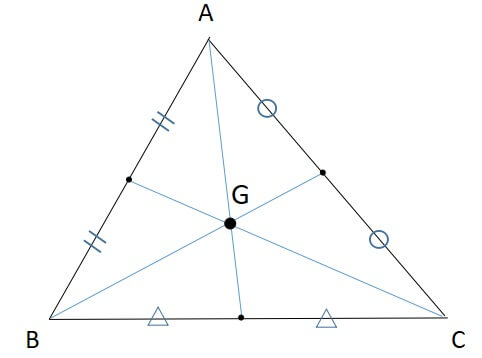
三角形の五心 内心 外心 重心 垂心 傍心 の性質と証明を解説

内心と外心の三角形の問題でテストの時にどっちかわからないように書いてあった時の見分け Clear

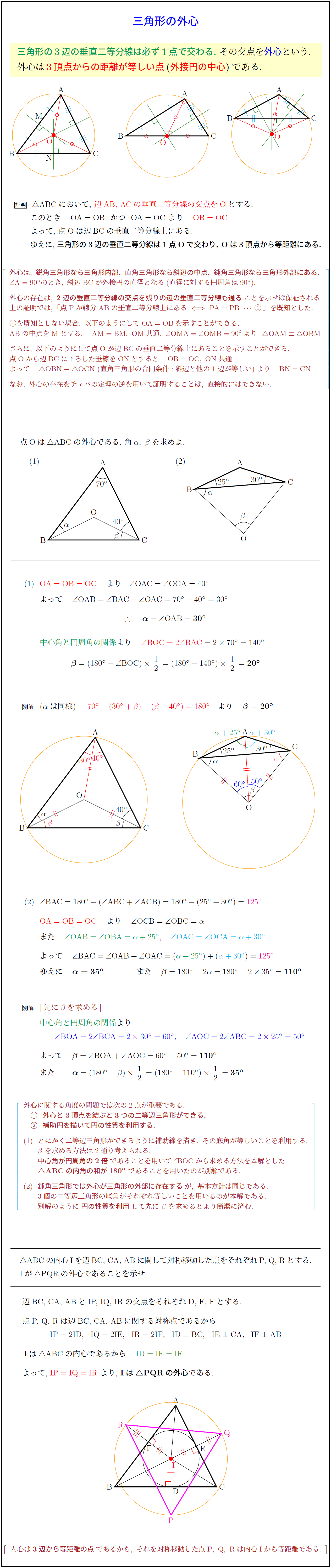
高校数学a 三角形の五心 三角形の外心とその存在証明 受験の月

内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学塾

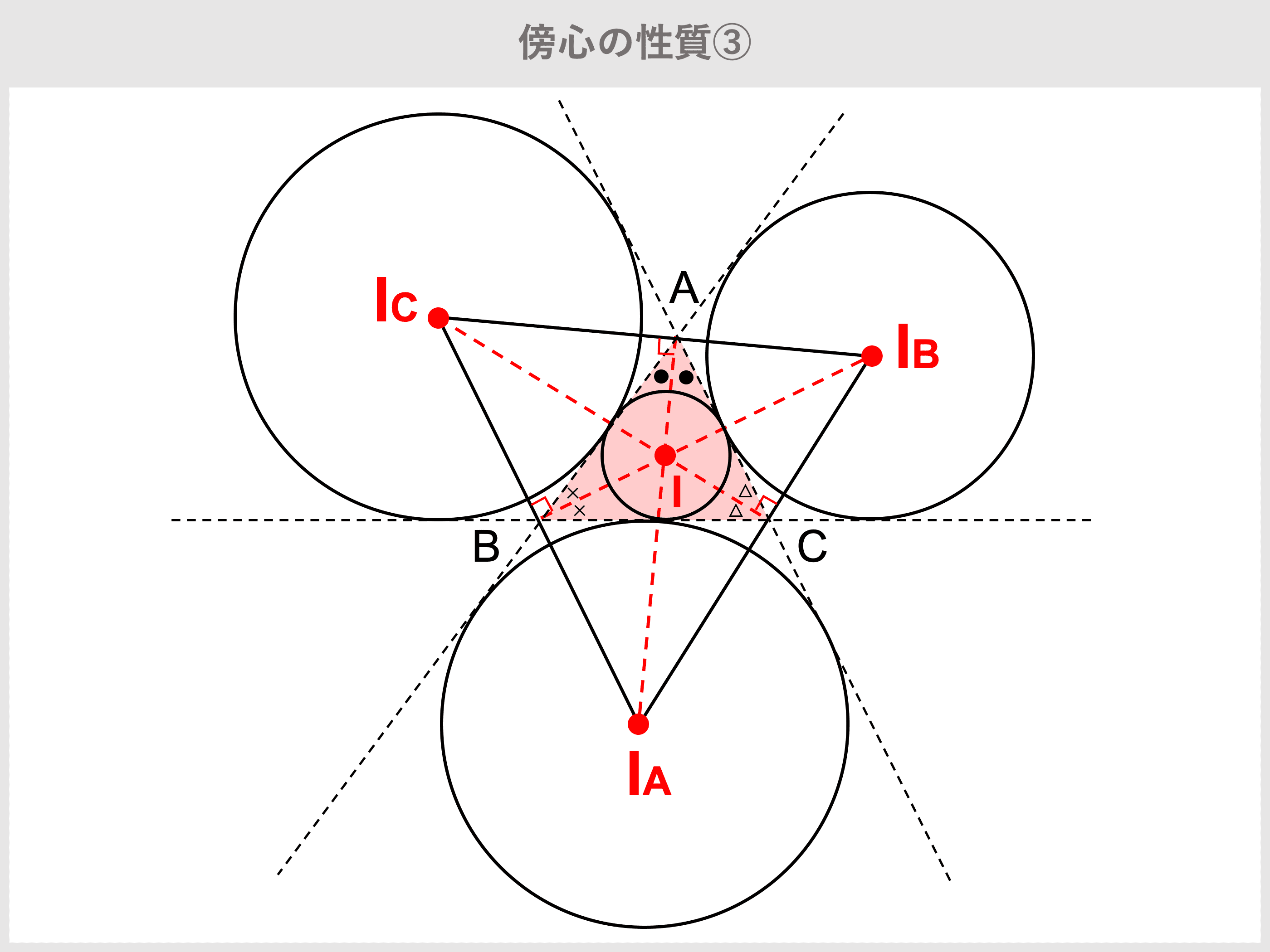
数学a 平面図形 三角形の性質 三角形の傍心

外心をo 内心をiとする Oiを求めよ Ab 8 7 Ca 5の三角形があり 数学 教えて Goo

三角形の内心 三角形の外心 三角形の重心

ベクトルと三角関数で表した内心 外心 重心 垂心

三角形の内心 高校数学ａ Youtube

クリアー数学ａ 数a P117 11 三角形の外心 内心 重心

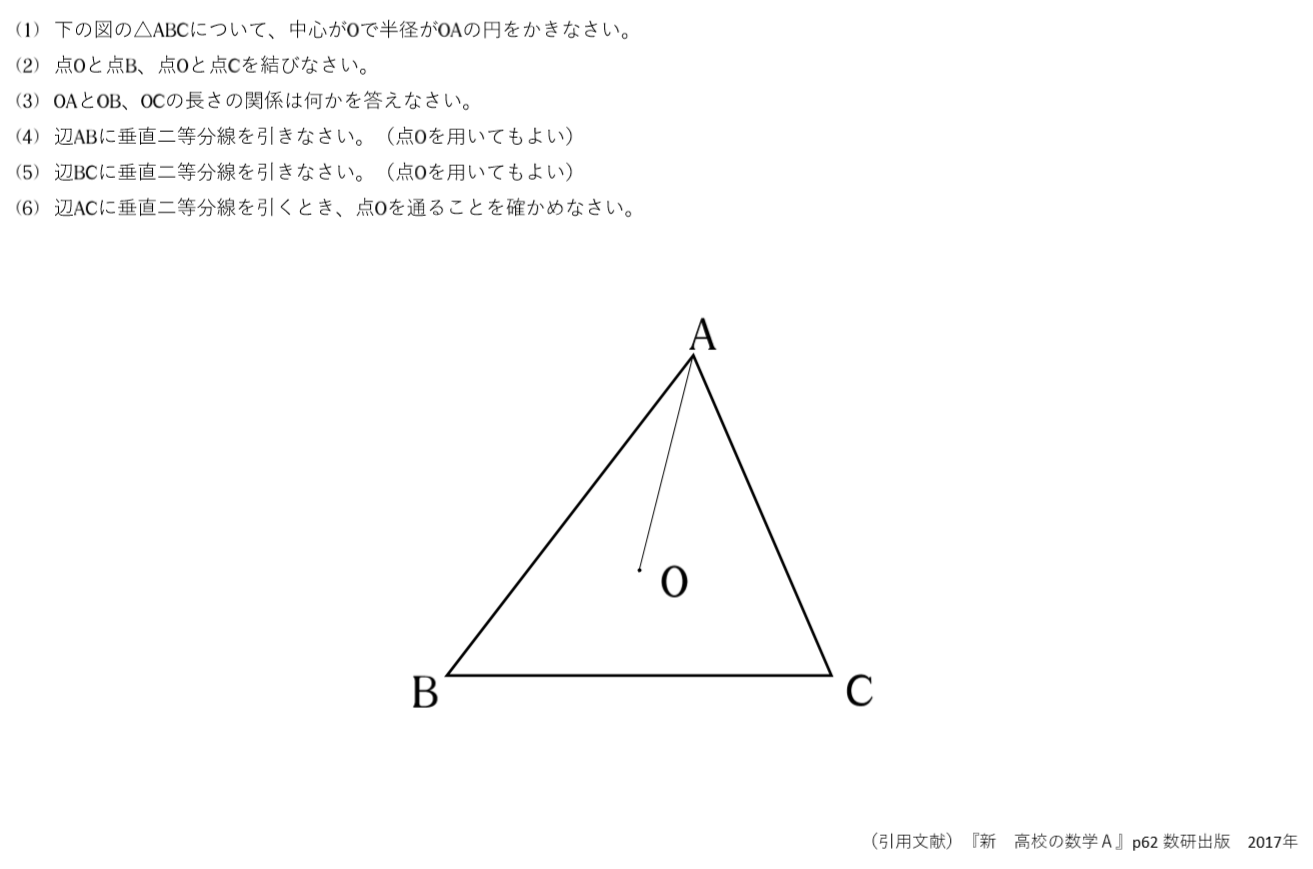
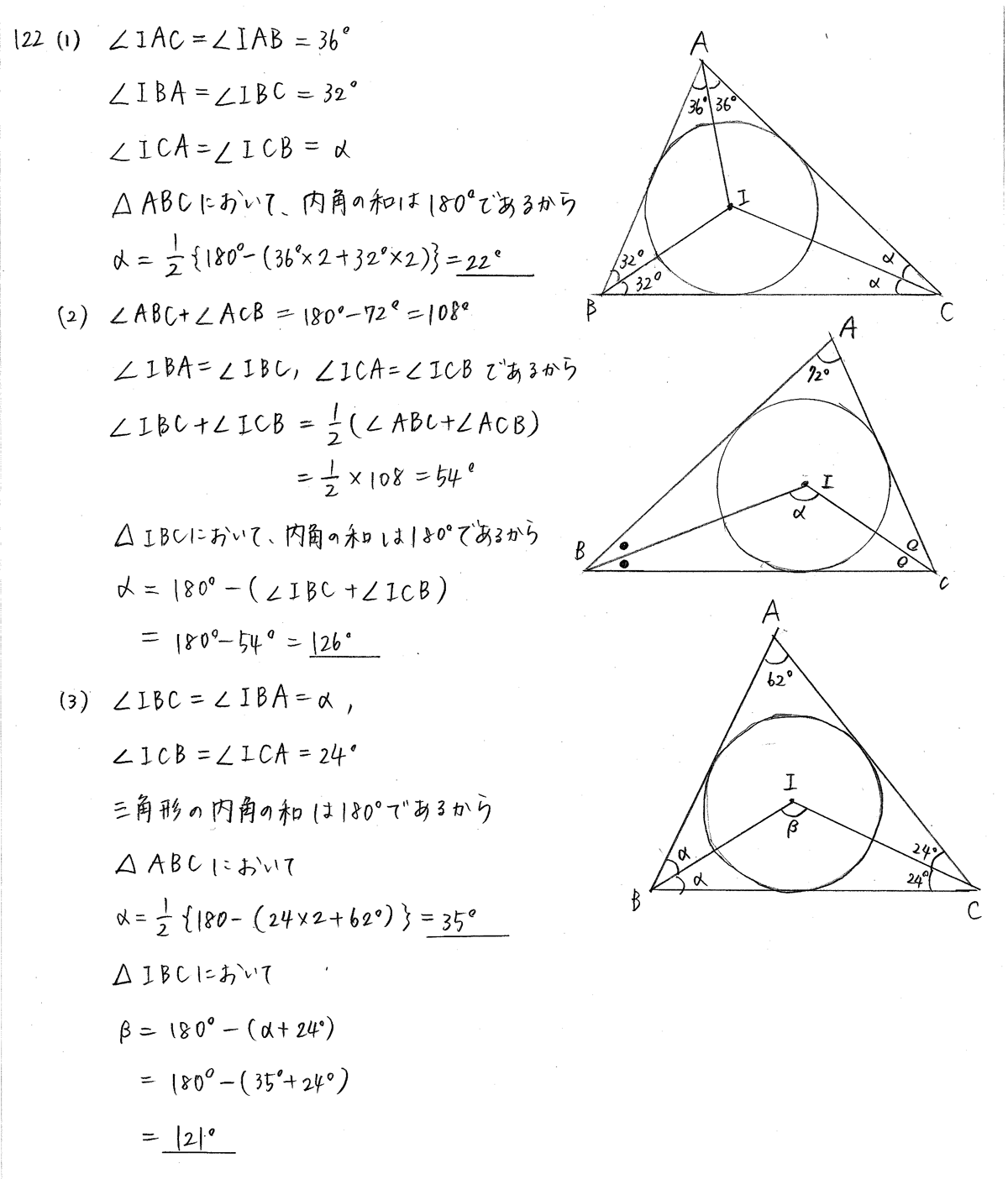
2講 三角形の外心 内心 重心 1節 平面図形 問題集 2章 図形の性質

数学a14三角形の外心 内心 重心 三角形にある有名な三つの中心 よく出てくるので覚えておきましょう ニコニコ動画

高校数学 数a 勉強動画 三角形の内心 外心 重心 垂心 の問題 19ch

三角形の外心について知っておきたい知識まとめ 理系ラボ

1枚目の写真が三角形の重心 外心です 2枚目の写真が三角形の内心 垂心です Clear

平面ベクトルと図形の問題 Of 京極一樹の数学塾会員頁

Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ

高校数学a 三角形の重心 外心 垂心の位置関係 オイラー線 の幾何的証明 受験の月

高校入試 三角形の内心 外心の問題 Youtube

ねこ騙し数学

外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学塾

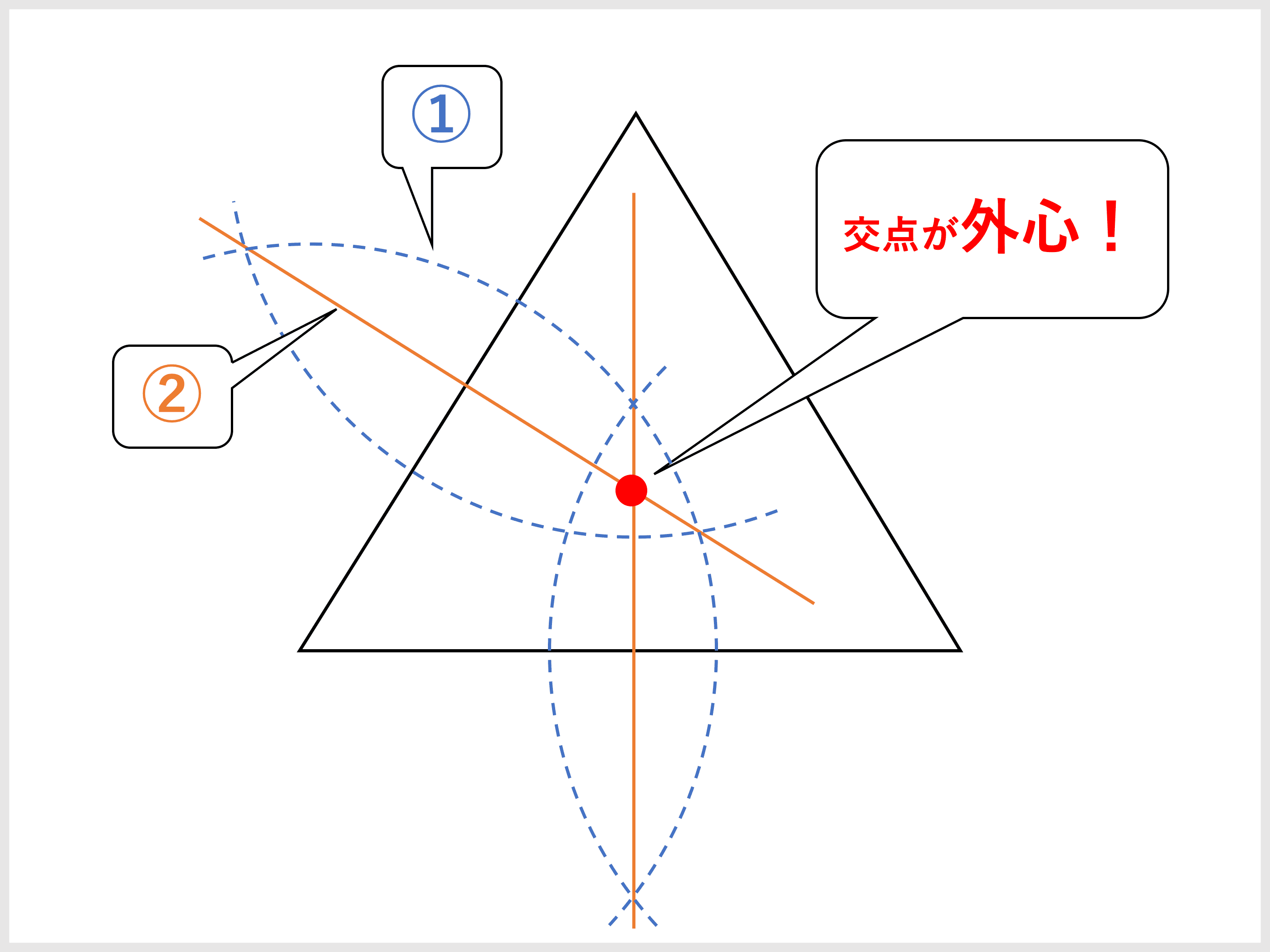
三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典

外接円 外心について

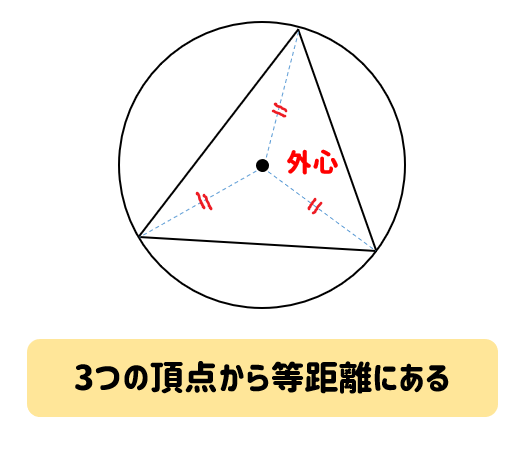
外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ

高校 数学 三角形の垂心 高校数学に関する質問 勉強質問サイト

三角形 内心 外心 垂心 重心 難関大学への数学

高校数学a 三角形の外心2 実践 練習編 映像授業のtry It トライイット

Incoming Term: 内心 外心 問題, 三角形の重心 内心 外心 問題,