70以上 30 60 90 right triangle side lengths 943335-Side lengths of a 30 60 90 right triangle
Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles , check out this 30 60 90 triangle tool and the calculator for special right triangles By Rich Zwelling, Apex GMAT Instructor Date 7th January, 21 Right Triangle In a previous piece, we covered the right triangle, also known as the isosceles right triangleThere is another socalled "special right triangle" commonly tested on the GMAT, namely the right triangle Like the isosceles right, its sides always fit a specific Solution This is a triangle in which the side lengths are in the ratio of x x√32x Substitute x = 7m for the longer leg and the hypotenuse ⇒ x √3 = 7√3 ⇒ 2x = 2 (7) =14 Hence, the other sides are 14m and 7√3m Example 6 In a right triangle, the hypotenuse is 12 cm, and the smaller angle is 30 degrees
Special Right Triangles Proof
Side lengths of a 30 60 90 right triangle
Side lengths of a 30 60 90 right triangle- 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a Worksheet 45 ¡45 ¡90 triangleand30 ¡60 ¡90 triangle 1For the 45 ¡45 ¡90 triangle, (the isosceles right triangle), there are two legs of length a and the



Special Right Triangles Proof
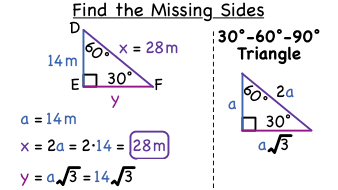
To find the side lengths of a one side must be given If the shorter side is given, multiply it by 2 to get the hypotenuse, and multiply it by the square root of 3 to get the longer sideA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is the shortest and the length of it is usually labeled as x The side opposite the 60º angle has a
We can see that this must be a triangle because we are told that this is a right triangle with one given measurement, 30° The unmarked angle must then be 60° Since 18 is the measure opposite the 60° angle, it must be equal toSpecial Right Triangles 30°60°90° triangle The 30°60°90° refers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be Definition of a triangles, including angles and side lengths A ??????
If you know the short leg length multiply by two for the hypotenuse length If you know the short leg then multiply by √3 for the long leg length If you know the long leg length divide by √3 for the short leg length The area of a triangle equals 1/2base * heightExample Given that the leg opposite the 30° angle for a triangle has a length of 12, find the length of the other leg and the hypotenuse The hypotenuse is 2 × 12 = 24 The side opposite the 60° angle isThen ABD is a 30°–60°–90° triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progression



1
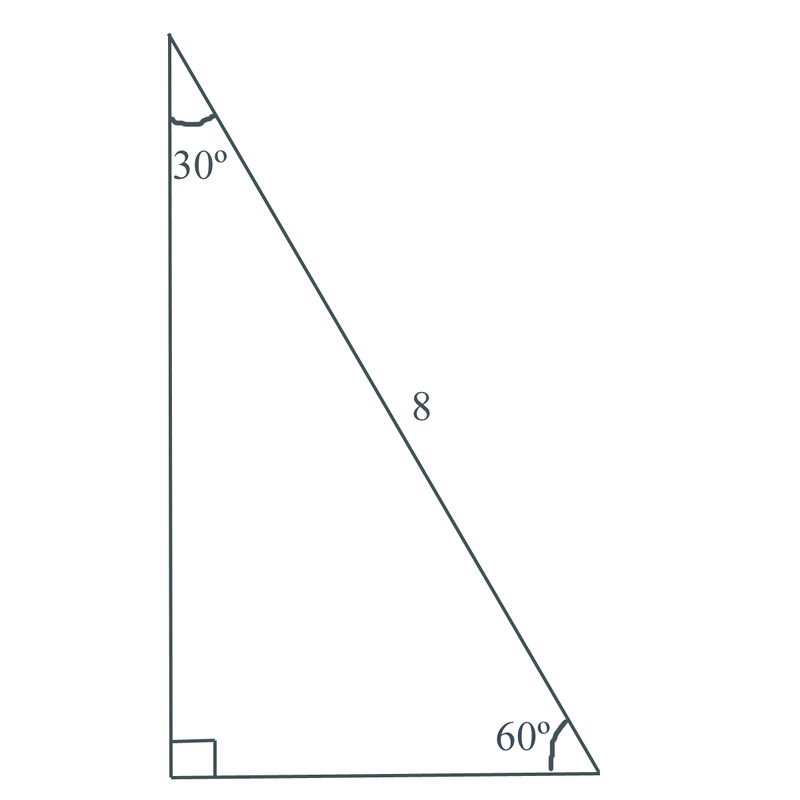



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
Answer (1 of 5) Why in a triangle is the the side opposite 60 degrees x (sqrt(3))?The 45 45 90The triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90° What Are the Side Lengths of a Triangle?
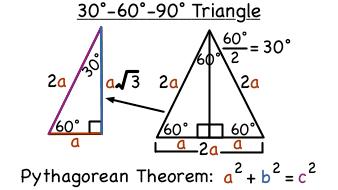



What Is A 30 60 90 Degree Triangle Virtual Nerd




30 60 90 Triangle Theorem Ratio Formula Video
A right triangle with a 30°angle or 60°angle must be a special right triangle Example 2 Find the lengths of the other two sides of a right triangle if the length of the hypotenuse is 8 inches and one of the angles is 30° Solution This is a right triangle with a triangle You are given that the hypotenuse is 830°60°90° Right Triangles All 30°60°90° Right Triangles are formed by taking half of a Equilateral Triange, as shown in the steps below Because the original triangle is Equilateral, that means all three sides are the same length This is what variable "x" is trying to tell you All three sides are the same lengthThe hypotenuse is the longest side in a right triangle, which is different from the long leg The long leg is the leg opposite the 60degree angle Two of the most common right triangles are and the degree triangles All triangles have sides



Which Could Be The Side Lengths Of A 30 60 90 Right Triangle Quora




Special Right Triangle Wikipedia
The sides of a triangle have a set patternThis is an isosceles right triangle The other triangle is named a triangle, where the angles in the triangle are 30 degrees, 60 degrees, and 90 degrees Common examples for the lengths of the sides are shown for each below The TriangleThe measures of the sides are x, x 3, and 2 x In a 30 ° − 60 ° − 90 ° triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is 3 times the length of the shorter leg
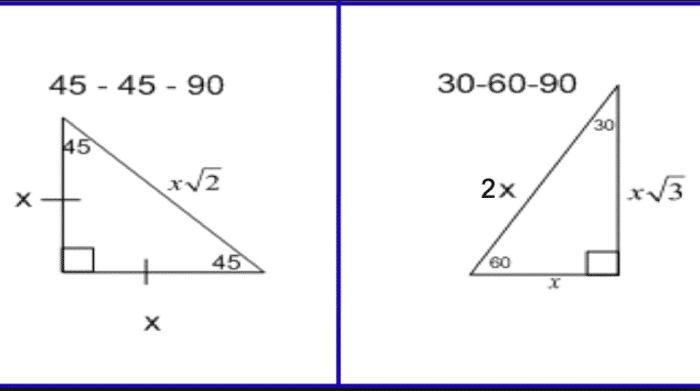



Special Right Triangles Complete Reference Guide The Education
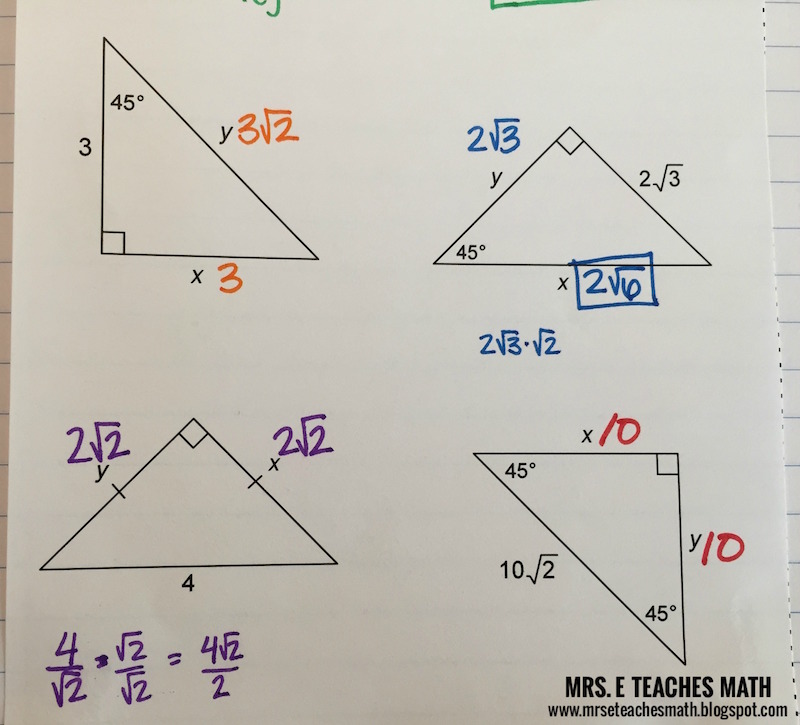



Right Triangles Interactive Notebook Pages Mrs E Teaches Math
The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2What I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is theWhat is the Formula?




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Ratio Formula Video
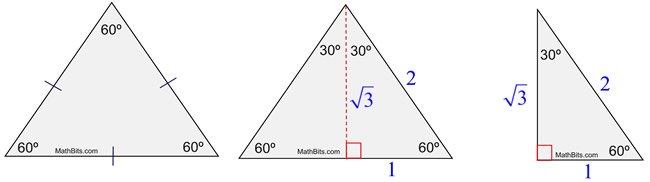
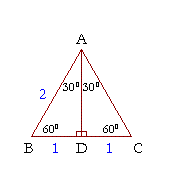
Find the missing side lengths Leave your answers as radicals in simplest form 1) 12 m n 30° 2) 72 ba 30° 3) x y 5 60° 4) x 133y 60° 5) 23 u v 60° 6) m n63 30° 7) a 53 b 60° 8) x 9 y 60° 9) 113x y 30° 10) 39 u v 30°If a side of the equilateral triangle is 2 units in length, then the side opposite the 30 o angle in one of the triangles is half that, or 1 unit, and the third side (the side opposite the 60 o angle) can be found by the Pythagorean Theorem In general, in a triangle, the side opposite the 30 o angle is half the hypotenuseSpecial right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangle



45 45 90 And 30 60 90 Triangles Zona Land Education



30 60 90 Triangle Rules
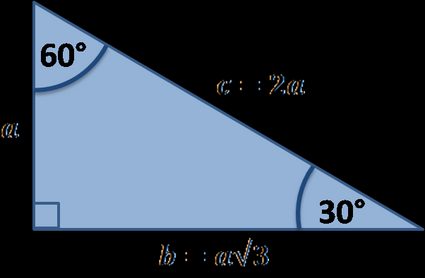
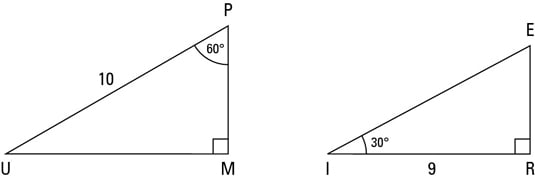
A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and the longer leg is the square root of 3 times the shorter legA special right triangle is one which has sides or angles for which simple formulas exist making calculations easy Of all these special right triangles, the two encountered most often are the 30 60 90 and the 45 45 90 triangles For example, a speed square used by carpenters is a 45 45 90The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5




A 30 60 90 Triangle Is Shown Below Find The Length Of The Side Labeled Y Brainly Com




Special Right Triangles Interactive Notebook Page 30 60 90 Mrseteachesmath Blogspot Co Trigonometry Worksheets Triangle Worksheet Math Interactive Notebook
It is based on bisecting an equilateral triangle and using the Pythagorean theorem A 30°60°90° triangle is formed when an equilateral triangle is bisected This makes the Hypotenuse a lengthThen ABD is a 30°–60°–90° triangle with hypotenuse of length 2, and base BD of length 1 The fact that the remaining leg AD has length √ 3 follows immediately from the Pythagorean theorem The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progressionLearn how to solve for the sides in a Special Right Triangle in this free math video tutorial by Mario's Math Tutoring009 What are the Ratios of t




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Right Triangles Solutions Examples Videos
Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units in A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherFind the length of the hypotenuse and the six trigonometric ratios sin 30° = cos 30° = tan 30° = csc 30° = sec 30° = cot 30° = sin 60° = cos 60° = tan 60° = csc 60° = sec 60° = cot 60




30 60 90 Triangle Definition Theorem Formula Examples



Right Triangles Gmat Free
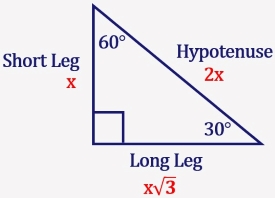
Given the triangle below, find the lengths of the missing sides Since this is a right triangle, we know that the sides exist in the proportion 1sqrt(3)2 The shortest side, 1, is opposite the 30 degree angle Since side X is opposite the 60 degree angle, we know that it is equal to 1*sqrt(3), or about 173 Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √ 3 Side opposite the 90° angle 2 xThe base and equal to half the size of the long side The remaining side is the triangles height Assigning 1 to the short half side, which is opposite 30 degrees, the long side, opposite 90, will be 2 The height, opposite 60 will be 3^ (1/2) —SQRT of 3 Any similar triangle can be derived by knowing one side




Which Set Of Values Could Be The Side Lengths Of A 30 60 90 Triangle Brainly Com




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
Is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across from the right angle The two special right triangles are right triangles with interior angles measuring 30 60 90 and 45 45 90 What is the 45 45 90 triangle rule?Triangle Ratio A degree triangle is a special right triangle, so it's side lengths are always consistent with each other The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x



Find The Side Lengths Of A Special Right Triangle 30 60 90 Mathondemand Com



Special Right Triangles Proof
A triangle is a right triangle with angles 30^@, 60^@, and 90^@ and which has the useful property of having easily calculable side lengths without use of trigonometric functions A triangle is a special right triangle, so named for the measure of its angles Its side lengths may be derived in the following manner👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio oThe reason these triangles are considered special is because of the ratios of their sides they are always the same!



How Do You Find Missing Sides In A 30a 60a 90a Triangle Virtual Nerd



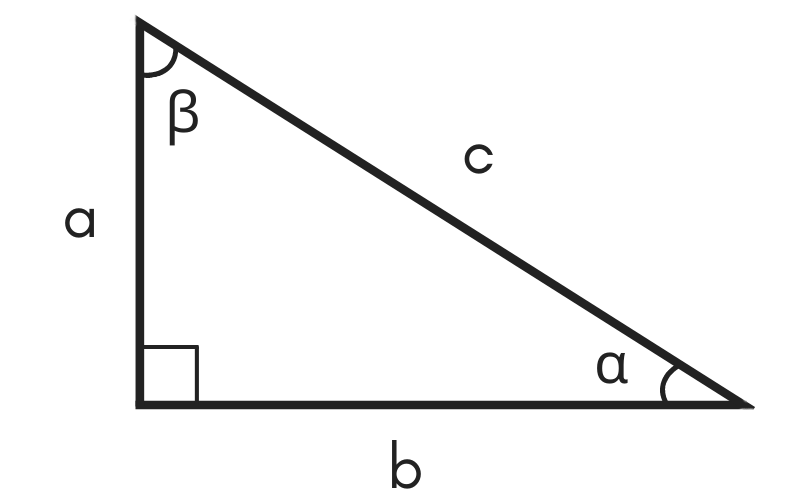
Trigonometry
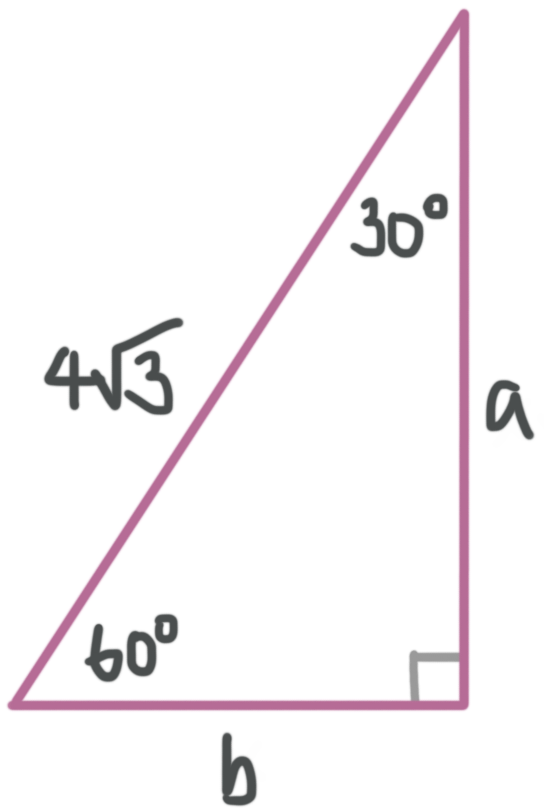
The lengths of the two sides of 30° – 60° – 90° Right Triangle are 4 inches and 4√3 inches;Here is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° anglesSpecial Right Triangle 30° 60° 90° Use the table below to remember the relationship of the 30°60°90° special right triangle Angle Measure 30° Step 1 Fill in the missing angle measures Step 2 Fill in the missing side lengths of each triangle, in simplest radical form 1 from Angle 90° 2 from Angle 6 Side Across from Angle x 60



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle Calculator Formula Rules
A degree triangle is a special right triangle, so its side lengths are always consistent with each other The ratio of the sides follow the triangle ratio given by the Formula as, 1 √3 2 Thus, for a triangle, the dimensions of the sides can be given as y = Short side



Identifying The 30 60 90 Degree Triangle Dummies




Special Right Triangles Review Article Khan Academy
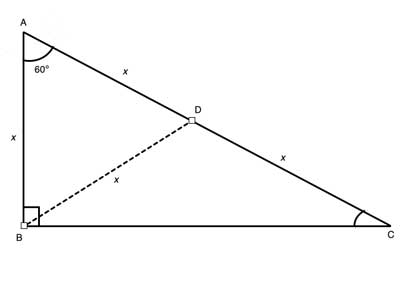



30 60 90 Triangle Geometry Help




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



The Easy Guide To The 30 60 90 Triangle
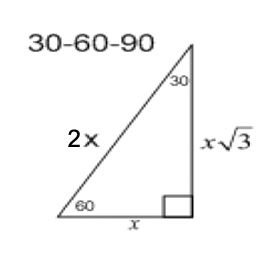



Special Right Triangles Geometry Quizizz
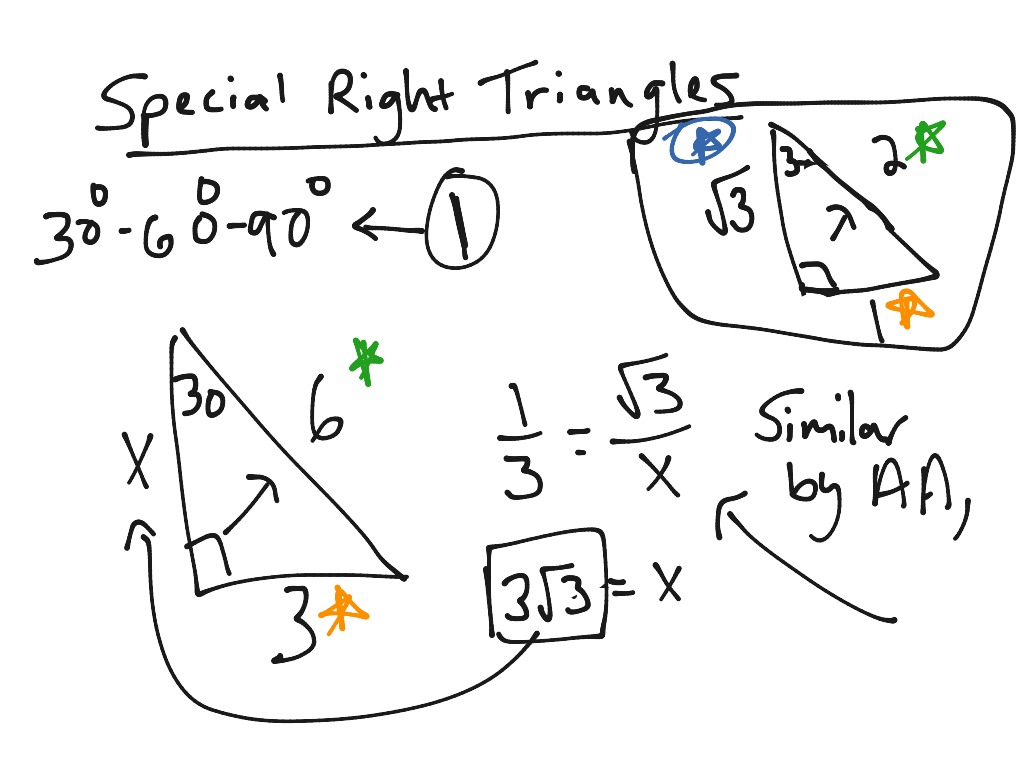



Special Right Triangles 30 60 90 Math Geometry Triangles Right Triangles Showme




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet
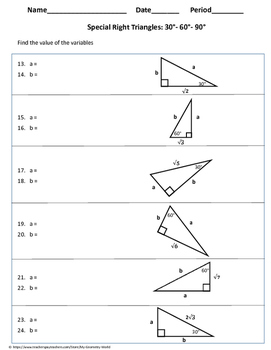



Geometry Worksheet 30 60 90 Triangles By My Geometry World Tpt




Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School



Special Right Triangle 30 60 45 45 37 53 Elearning




Special Right Triangles Fully Explained W 19 Examples




Learn About The 30 60 90 Triangle Caddell Prep Online




Special Right Triangles Video Lessons Examples And Solutions



4 43 30 60 90 Right Triangles K12 Libretexts




Right Triangles Special Right Tris Notes Practice Task Cards Riddle Bundle Special Right Triangle Right Triangle Math Notes




30 60 90 Triangles




30 60 90 Triangle Formulas Rules And Sides Science Trends
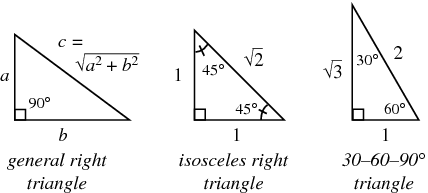



Right Triangle From Wolfram Mathworld




Solved Mush Precalculus Name Warmup Date Speial Right Chegg Com



The Easy Guide To The 30 60 90 Triangle




5 8 Special Right Triangles



Geometry Problem 963 Right Triangle 30 60 90 Degrees Angle Bisectors Metric Relations Math Teacher Master Degree School College Sat Prep Elearning Online Math Tutor Lms



30 60 90 Triangle Formulas Rules And Sides Science Trends




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube




30 60 90 Triangle Theorem Ratio Formula Video



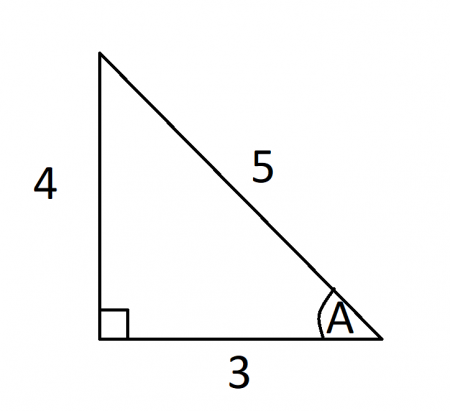
Is A 3 4 5 Triangle Also A 30 60 90 Triangle Quora



30 60 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Right Triangle Side Ratios Expii




30 60 90 45 45 90 Special Right Triangles Youtube




30 60 90 Triangle Calculator Formula Rules




The Complete Guide To The 30 60 90 Triangle




Special Right Triangles 30 60 90 Ck 12 Foundation




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangles Spock S Guide To Math 4




Solved Special Right Triangles 30 Degree 60 Degree 90 Chegg Com




How To Use The Special Right Triangle 30 60 90 Studypug




Special Right Triangles Part 3 30 60 90 Youtube




30 60 90 Triangle Explanation Examples




Velocity




How To Work With 30 60 90 Degree Triangles Education Is Around



How To Solve 30 60 90 Triangles Krista King Math Online Math Tutor




30 60 90 Right Triangles Free Math Help




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Special Right Triangles Exploration 30 60 90 And 45 45 90 Full Package




30 60 90 Triangle Theorem Ratio Formula Video



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




Geometry Notes Pythagorean Thm Special Right Triangles 30 60 90 Triangles



30 60 90 Right Triangle Side Ratios Expii
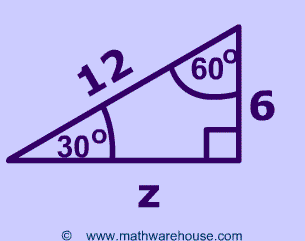



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




Triangles And Lines Special Right Triangles There Are Two Special Right Triangles 30 60 90 Degree Right Triangle 45 45 90 Degree Right Triangle Ppt Download




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Ratio Formula Video




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Theorem Ratio Formula Video
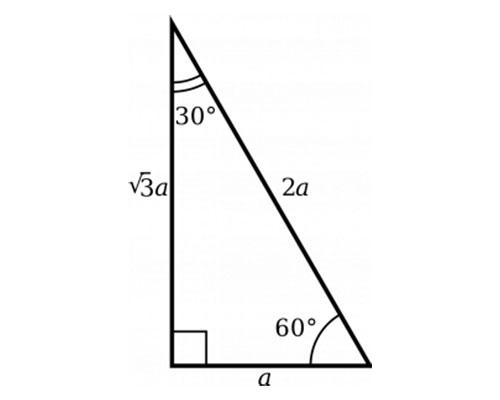



30 60 90 Triangle Sides Examples Angles Full Lesson



1




30 60 90 Right Triangles Read Geometry Ck 12 Foundation




The Complete Guide To The 30 60 90 Triangle
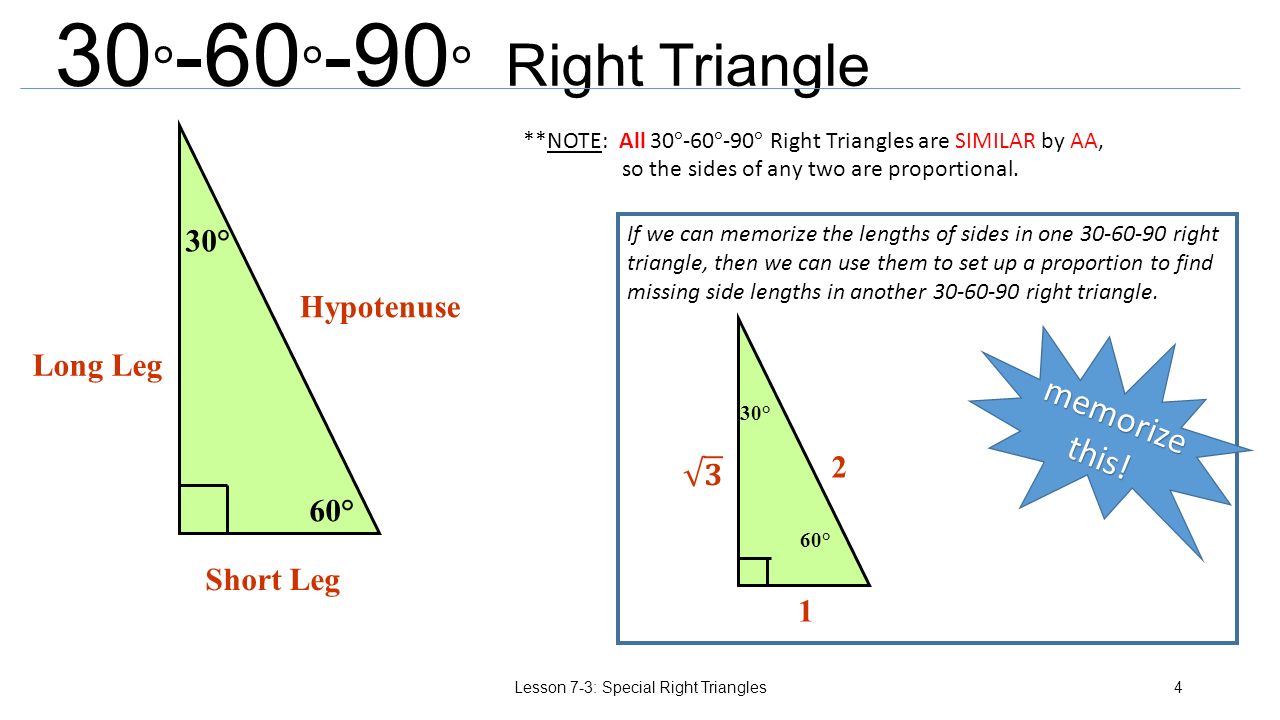



Special Right Triangles Lesson 7 3 Special Right Triangles1 Ppt Download




30 60 90 Right Triangles Read Geometry Ck 12 Foundation
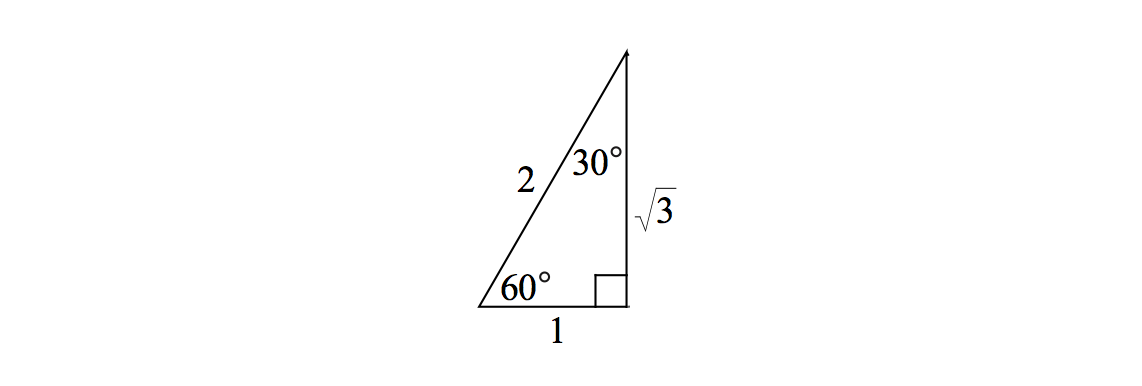



Lengths In Right Triangles Brilliant Math Science Wiki




Special Right Triangles Review Article Khan Academy
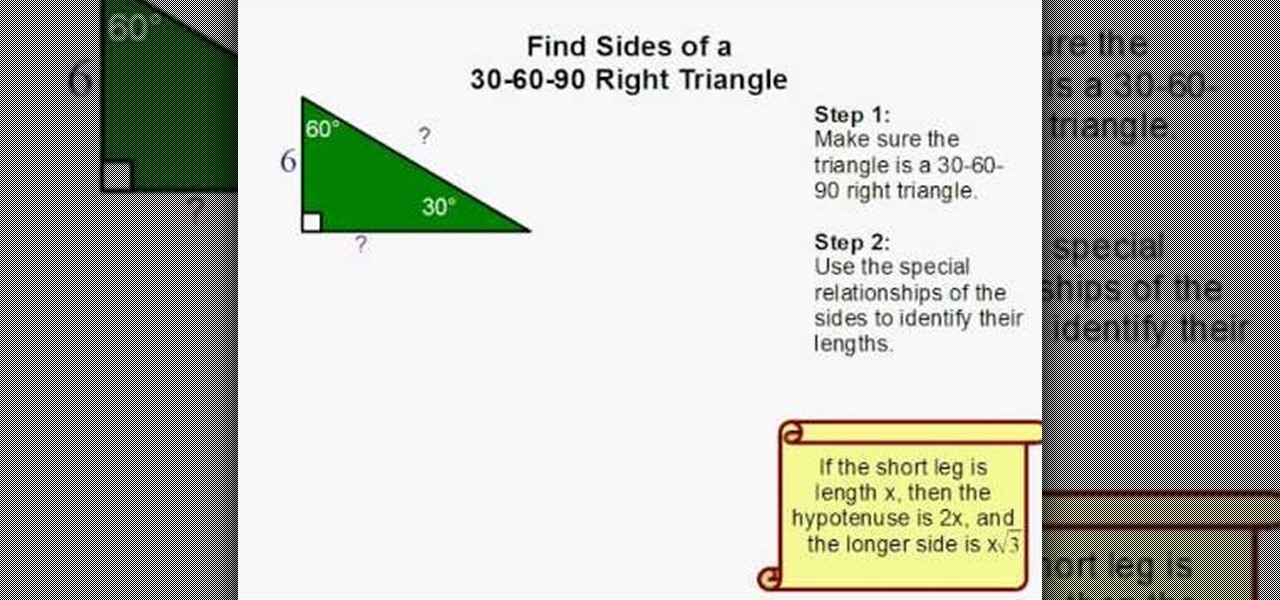



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto
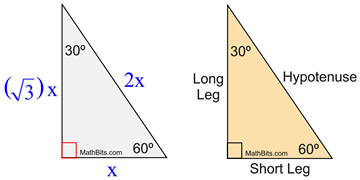



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
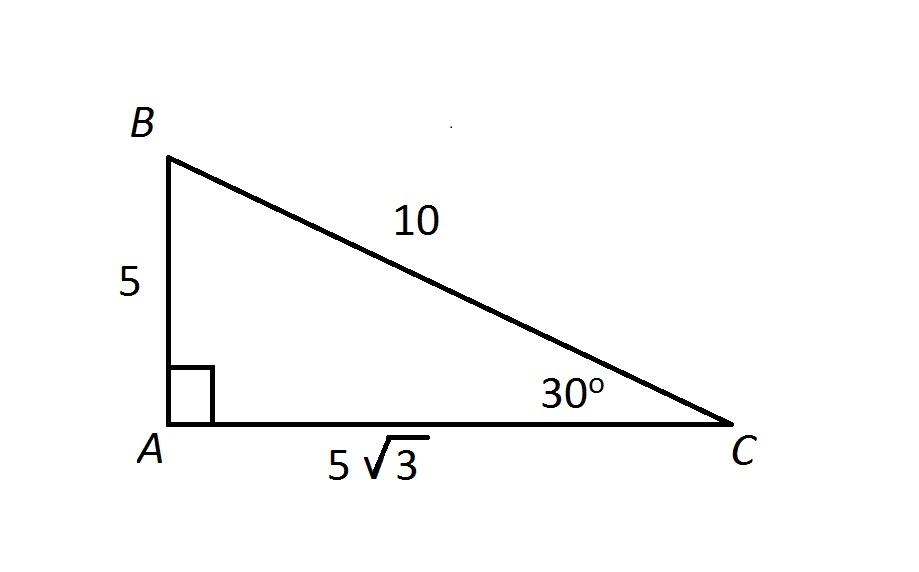



Special Triangles Hiset Math



1
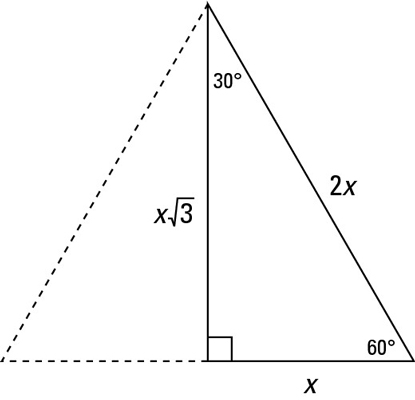



Identifying The 30 60 90 Degree Triangle Dummies




The 30 60 90 Triangle Topics In Trigonometry




Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math



1



30 60 90 Right Triangles Consider The Following




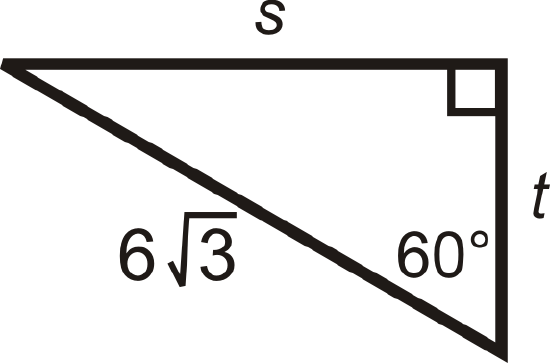
I M The 30 60 90 Triangle Below Side S Has A Length Of And The Hypotenuse Has A Length Of Brainly Com




30 60 90 Triangle Explanation Examples




Math Example Right Triangles Example 25 Media4math



Right Triangles Gmat Free




30 60 90 Special Right Triangle Calculator Inch Calculator



コメント
コメントを投稿